Coefficient of Friction between a Body and Wedge
The coefficient of friction is a number which represents the friction between two surfaces. Between two equal surfaces, the coefficient of friction will be the same. The symbol usually used for the coefficient of friction is μ.
A body slides on a smooth wedge of angle θ and its time of descents is t. if the same wedge made rough then time taken by it to come down becomes n times more (i.e., nt). The lengths of path in both the cases are same.
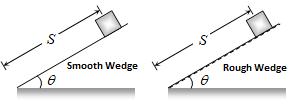
For smooth wedge, S = ut + ½ at².
S = ½ (g sin θ) t² … (1) (As u = 0 and a = g sin θ)
For rough wedge, S = ut + ½ at²
S = ½ g (sin θ – μ cos θ) (nt)² … (2) [As u = 0 and a = g (sin θ – μ cos θ)]
From equations (1) and (2) we get:
½ (g sin θ) t² = ½ g (sin θ – μ cos θ) (nt)²
sin θ = (sin θ – μ cos θ) n²
Coefficient of friction (μ) = \(\tan \theta \left( 1-\frac{1}{{{n}^{2}}} \right)\).
