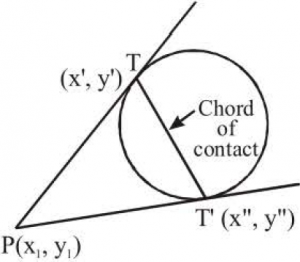
Chord of Contact and Chord
Bisected at a given Point: The chord joining the points of contact of the two tangents to a conic drawn from a given point, outside it, is called the chord of contact of tangents.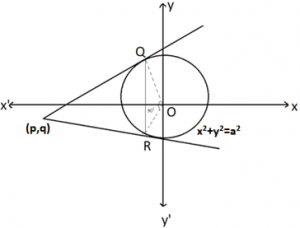
The equation of the chord of contact of tangents drawn from a point (x₁, y₁) to the circle x² + y² = a² is xx₁ + yy₁ = a²
- The equation of the chord of contact is of the same form as the equation of the tangent, if the point lies on the conic.
Remark: The equation of the chord of contact or tangent drawn at a point (x₁, y₁) to the circle x² + y² + 2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x + x₁) + f(y + y₁) + c = 0.
Example: If the chord of contact of tangents drawn from a point (p, q) to the circle x² + y² = a² subtends a right angle at the center of the circle, then prove that p² + q² = a²
Solution: The equation of the chord of contact of tangents drawn from (p, q) to the circle x² + y² = a² is px + qy = a² … 1
The combined equation of OQ and OR is a homogenous equation of second degree obtained with the help of x² + y² = a² and (1) and is given by \({{x}^{2}}+{{y}^{2}}={{a}^{2}}{{\left[ \frac{px+qy}{{{a}^{2}}} \right]}^{2}}\)
a²(² + y²) = (px + qy)²
Lines given by this equation are mutually perpendicular.
Therefore,
Coefficient of x² + Coefficient of y² = 0
p² – a² + q² – a² = 0
p² + q² = 2a²
Chord Bisected at a given point: The equation of the chord of the circle x² + y² = a² bisected at the point (x₁, y₁) is given by is xx₁ + yy₁ – a² = x₁² + y₁² – a² or T = S’.
Where T and S’ have their usual meanings.
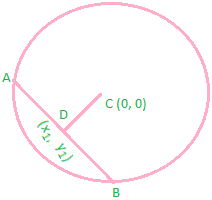
Example: Find the locus of the middle points of the chords of the circle x² + y² = a² which subtend a right angle at the center.
Solution: Let (h, k) be the midpoint of a chord AB of the circle x² + y² = a² Then, the equation of AB is hx + ky – a² = h² + k² – a²
Or hx + ky = h² + k² … (1)
The combined equation of OA and OB is \({{x}^{2}}+{{y}^{2}}={{a}^{2}}{{\left[ \frac{hx+ky}{{{{h}^{2}}}+{{{k}^{2}}}} \right]}^{2}}\)
Or (h² + k²) (x² + y²) – a² (hx + ky)²
OA and OB will be perpendicular if Coefficient of x² + Coefficient of y² = 0
(h² + k²)² – a²h² + (h² + k²)² = 0,
2(h² + k²)² – a² (h² + k²) = 0,
2(h² + k²) – a² = 0,
So, locus of (h, k) is 2(h² + k²) – a² = 0.