The branch of the physical chemistry which deals with the rate at which the chemical reactions occurs, the mechanism by which the chemical reaction occurs and the effect of various factors like pressure, concentration, temperature on the reaction rates is called the chemical kinematics.
Effects of temperature on the Rate of Reaction:
⇒ The rate of a chemical reaction increases with increasing the temperature.
⇒ A collision between reactant molecules must occur with a minimum energy before effective yielding product molecules. This is called the activation energy (Ea).
⇒ The temperature coefficient of a chemical reaction is defined as the ratio of the specific reaction rates of a reaction at two temperatures differing by 10°C.
\(\mu =\frac{{{k}_{t}}+10}{{{k}_{t}}}\).
\(\frac{{{k}_{{{T}_{2}}}}}{{{k}_{{{T}_{1}}}}}=\mu \frac{({{T}_{2}}-{{T}_{1}})}{10}=\mu \frac{\Delta T}{10}\).
\(\log \left[ \frac{{{k}_{{{T}_{2}}}}}{{{k}_{{{T}_{1}}}}} \right]=\frac{\Delta T}{10}\log \mu \).
⇒ The larger the value of Ea, the smaller the value of rate constant.
⇒ At lower temperatures, an increase in temperature causes more than a change in the value of k than that at higher temperatures.
Arrhenius equation:
A variation of the rate constant k with temperature T (k) is given by Arrhenius equation.
\(k=A.{{e}^{-\frac{Ea}{RT}}}\).
\(\ln \,k=\ln \,A-\frac{Ea}{RT}\).
\(\log k=\log A-\frac{Ea}{2.303R}\).
A is called the frequency factor.
A & Ea are called as Arrhenius parameters.
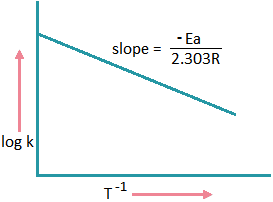
If we plot a graph between log k and 1/T
we get a straight line with
\(slope=-\frac{Ea}{2.303R}\).
Ea = 2.303 x R x slope
\(\log \frac{{{k}_{2}}}{{{k}_{1}}}=\frac{Ea}{2.303R}\left[ \frac{{{T}_{2}}-{{T}_{1}}}{{{T}_{1}}{{T}_{2}}} \right]\).
