Bohr’s Theory of Hydrogen Atom
Niels Bohr suggested that the problem about hydrogen spectrum can be solved if we can make some assumptions. According to classical theory, the frequency of the electromagnetic waves emitted by a revolving electron is equal to the frequency of revolution. As the electrons radiate energy, their angular velocities would change continuously and they would emit a continuous spectrum against line spectrum actually observed. So, Bohr concluded that even if electromagnetic theory successfully explained the macroscopic phenomenon, it could not be applied to explain microscopic phenomenon, that in atomic scale. So he made bold suggestions called as Bohr’s postulates.
To explain the energy levels, Bohr developed a model in which the electron has certain allowed orbits and the jump between energy levels corresponded to the electron moving from one allowed orbit to another. The classical hydrogen atom with Rutherford’s discovery of the atomic nucleus, it became clear that atoms consisted of a positively charged nucleus surrounded by negatively charged electrons that were held to the nucleus by an electric force. The simplest atom would be hydrogen consisting of one proton and one electron held together by a coulomb force of magnitude.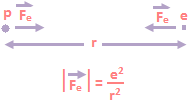
As shown in the above equation, both the proton and the electron attract each other, but since the proton is 1836 times more massive than the electron, the proton should sit nearly at rest while the electron orbits around it. The side view of circular motion is an up and down oscillation.
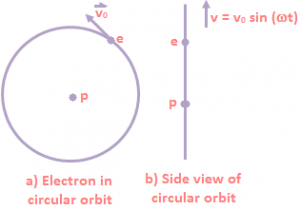Thus the hydrogen atom is such a simple system, with known masses and known forces, that it should be a straightforward matter to make detailed predictions about the nature of the atom. We could use the orbit program, replacing the gravitational force \(\frac{GMm}{{{r}^{2}}}\) by \(\frac{{{e}^{2}}}{{{r}^{2}}}\). We would predict that the electron moved in an elliptical orbit about the proton, obeying all of Kepler’s laws for orbital motion. There is one important point we would have to take into account in our analysis of the hydrogen atom that we did not have to worry about in our study of satellite motion. The electron is a charged particle, and accelerated charged particles radiate electromagnetic waves. Suppose, for example, that the electron were in a circular orbit moving at an angular velocity ω as shown in Figure (a). If we were looking at the orbit from the side, as shown in Figure (b), we would see an electron oscillating up and down with a velocity given by v = v₀ sinωt.
If electrons oscillated up and down at a frequency ω, they produced radio waves of the same frequency. Thus it is a prediction of Maxwell’s equations that the electron in the hydrogen atom should emit electromagnetic radiation, and the frequency of the radiation should be the frequency at which the electron orbits the proton.
For an electron in a circular orbit, predicting the motion is quite easy. If an electron is in an orbit of radius r, moving at a speed v, then its acceleration a is directed toward the centre of the circle and has a magnitude \(\overrightarrow{a}\,=\,\frac{{{v}^{2}}}{r}\).
Using Equations of the electric force and the acceleration, and noting that the force is in the same direction as the acceleration, as indicated in the above figure, Newton’s second law gives \(\left| {\vec{F}} \right|\,=\,m\,\left| {\vec{a}} \right|\).
\(\frac{{{e}^{2}}}{{{r}^{2}}}\,=\,m\,\frac{{{v}^{2}}}{r}\).
One factor of r cancels and we can immediately solve for the electron’s speed v to get \({{v}^{2}}\,=\,\frac{{{e}^{2}}}{mr}\) or \({{v}_{electron}}\,=\,\frac{e}{\sqrt{mr}}\).
The period of the electron’s orbit should be the distance 2πr travelled, divided by the speed v or \(\frac{2\pi r}{v}\) seconds per cycle and the frequency should be the inverse of that \(\frac{v}{2\pi r}\) cycles per second. Using the above equation for v, we get Frequency of electron in orbit \(=\,\frac{v}{2\pi r}\,=\,\frac{e}{2\pi \sqrt{mr}}\).
According to Maxwell’s theory, this should also be the frequency of the radiation emitted by the electron.