Angle of Elevation and Depression of A Point
Suppose a straight-line AX is drawn in the horizontal direction. Then the angle XAP where P is a point above AX is called the angle of elevation of P as seen from A. similarly the angle XAQ where Q is below AX, is called the angle of depression of some point Q.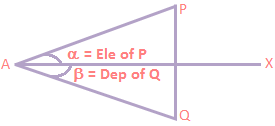
Any line perpendicular to a plane is perpendicular to energy line lying in the plane.
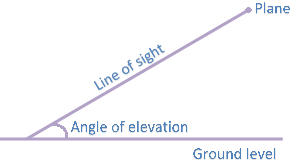To express one side of a right-angled triangle in terms of the other side.
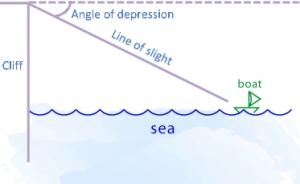Let <ABC = q, where ABC is a right-angled triangle in which <C = 90.
The side opposite right angle C will be denoted by H (hypotenuse), the side opposite to angle will be denoted by O (opposite) and the side containing the angle q (other than H) will be denoted by A i.e., adjacent side.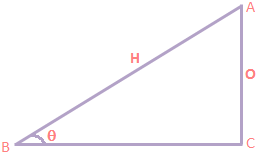
Then from the figure it is clear that
O = A (tanq)
I.e., opposite = Adj (tanq)
Also O = H (sinq) or A = H (cosq)
Or opposite = Hyp (sinq)
Or Adj = Hyp (cosq)
Geometrical Properties for A Triangle: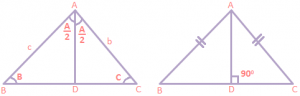
(i) In a triangle the internal bisector of an angle divides the opposite side in the ratio of the arms of the angle \(\frac{BD}{DC}=\frac{c}{b}\).
(ii) In an isosceles triangle the median is perpendicular to the base.
(iii) In similar triangles the corresponding sides are proportional.
(iv) The exterior angle is equal to sum of interior opposite angles.
q = A + B
Example: A ladder rests against a wall at an angle X to the horizontal its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal, show that \(a=b\,\tan \left( \frac{\alpha +\,\beta }{2} \right)\).
Solution: b = BC= AB – AC = lsinβ – l sinα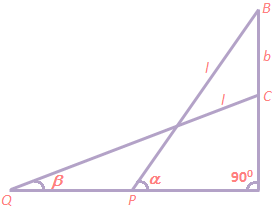
A = PQ = AQ – AP = l cos β – l cosα
∴ \(\frac{a}{b}=\frac{\cos \alpha -\cos \beta }{\sin \beta -\sin \alpha }=\tan \left( \frac{\alpha +\beta }{2} \right)\).