Biot – Savart Law and Its Applications
Two French physicists, Jean Baptiste Biot and Felix Savart derived the mathematical expression for magnetic flux density at a point due a nearby current carrying conductor, in 1820. Viewing the deflection of a magnetic compass needle, two scientists concluded that any current element projects a magnetic field in the space.
After, through observations and calculations they had derived a mathematical expression, which shows the magnetic flux density of which dB, is directly proportional to the length of the element dl, the current I, the sine of the angle and θ between direction of the current and the vector joining a given point of the field and the current element and is inversely proportional to the square of the distance of the given point from the current element r. This is Biot Savart law statement.
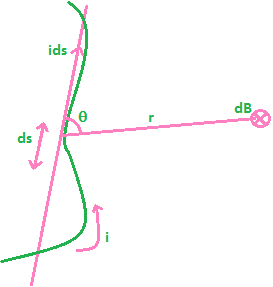
The Biot-Savart’s law gives the magnetic field produced due to a current carrying segment. This segment is taken as a vector quantity known as the current element.
Consider a wire carrying a current i in a specific direction as shown in the above figure. Take a small element of the wire of length ds. The direction of this element is along that of the current so that it forms a vector ids. If we wish to know the magnetic field produced at a point due to this small element, then we can use the Biot-Savart’s Law. Let the position vector of the point in question drawn from the current element be r and the angle between the two be θ. Then,
\(dB\,=\,\frac{{{\mu }_{0}}}{4\pi }\,\frac{i\,ds\,\sin \theta }{{{r}^{2}}}\).
Where,
μ₀ = Permeability of free space = 4π x 10⁻⁷ m/A.
The direction of the magnetic field is always in a plane perpendicular to the line element and position vector. It is given by the right hand thumb rule where the thumb points to the direction of conventional current and the other fingers show the magnetic field directions.
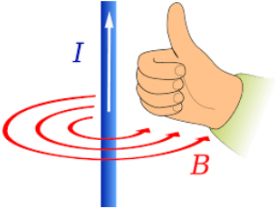
In the figure shown above the direction of magnetic field is pointing into the page.
This can be expressed in terms of vectors as:
\(\overrightarrow{dB}\,=\,\frac{{{\mu }_{0}}}{4\pi }\,\frac{i\,\overrightarrow{ds}\times r}{{{r}^{2}}}\).
Let us use this law in an example to calculate the Magnetic field due to a wire carrying current in a loop.
Example: Magnetic field of Current Loop.
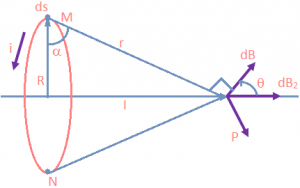
Consider a current loop of radius R with a current is flowing in it. If we wish to find the electric field at a distance l from the centre of loop due to a small element ds, we can use the Biot- Savart Law as \(\overrightarrow{dB}\,=\,\frac{{{\mu }_{0}}}{4\pi }\,\frac{i\,\overrightarrow{ds}\times \widehat{r}}{{{r}^{2}}}\).
Consider the current element ids at M which is coming out of plane in the figure. Since r is in plane of the page, the two of them are perpendicular to each other. Furthermore, the magnetic field produced dB.
\(dB\,=\,\frac{{{\mu }_{0}}}{4\pi }\,\frac{i\,\times \,ds\,\times \,1\,\times \,\sin {{90}^{0}}}{{{r}^{2}}}\,=\frac{{{\mu }_{0}}}{4\pi }\,\times \,\frac{i\,\,\times \,ds}{{{r}^{2}}}\).
But from the figure,
R² + l² = r²
\(dB\,=\,\frac{{{\mu }_{0}}}{4\pi }\times \frac{i\,\times \,ds}{{{R}^{2}}\,+\,{{l}^{2}}}\,\).
Now if we consider the diametrically opposite element at N, it produces a field such that its component perpendicular to the axis of the loop is opposite to that of the field produced at M. Thus only the axial components remain. We can divide the loop into diametrically opposite pairs and apply the same logic.
Also note that from figure that:
α = θ
∴ cosθ = \(\frac{R}{\sqrt{{{R}^{2}}\,+\,{{l}^{2}}}}\),
\(dB\,\cos \,\theta \,=\,\frac{{{\mu }_{0}}}{4\pi }\,\times \,\frac{i.ds}{{{R}^{2}}\,+\,{{l}^{2}}}\,\times \,\frac{R}{\sqrt{{{R}^{2}}\,+\,{{l}^{2}}}}\).
The total field will be thus
\(B\,=\,\int{\frac{{{\mu }_{0}}}{4\pi }}\,\times \,\frac{i\,\times \,ds\,\times \,R}{{{\left( {{R}^{2}}\,+\,{{l}^{2}} \right)}^{3/2}}}\,=\,\frac{{{\mu }_{0}}}{4\pi }\,\times \,\frac{i\,R}{{{\left( {{R}^{2}}\,+\,{{l}^{2}} \right)}^{3/2}}}\int{ds}\),
\(B\,=\,\frac{{{\mu }_{0}}}{4\pi }\,\times \,\frac{i\,\times \,R}{{{\left( {{R}^{2}}\,+\,{{l}^{2}} \right)}^{3/2}}}\,\times \,2\pi R\),
\(B\,=\,\frac{{{\mu }_{0}}\,i\,{{R}^{2}}}{2{{\left( {{R}^{2}}\,+\,{{l}^{2}} \right)}^{3/2}}}\).
