Acceleration in Simple Harmonic Motion
Simple Harmonic Motion is any motion where a restoring force is applied that is proportional to the displacement and in the opposite direction of that displacement.
(1) The acceleration of the particle executing S.H.M at any instant is defined as the rate of change of its velocity at that instant so
Acceleration\(\left( A \right)=\frac{dv}{dt}=\frac{d}{dt}\left( a\omega \cos \omega t \right)\) = – ω² a sinωt = – ω²y … (1) [As y = a sin ωt].
(2) In Simple Harmonic Motion as |Acceleration| = ω²y … (2), is not constant. So, equations of translator motion can’t be applied.
(3) In Simple Harmonic Motion acceleration is maximum at extreme position (at y = ± a), Hence |Amax| = ω²a when |sin ωt| = Maximum = 1 i.e.., at \(t=\frac{T}{4}\) (or) \(\omega t=\frac{\pi }{2}\).
From equation (2): |Amax| = ω²a when y = a.
(i) In Simple Harmonic Motion acceleration is minimum at mean position, from equation (1): Amin = 0 when sin ωt = 0 i.e.., at t = 0 (or) \(t=\frac{T}{2}\) (or) ωt = π. From equation (ii): Amin = 0 when y = 0.
(ii) Acceleration is always directed towards the mean position and so is always opposite to displacement. i.e.., A α – y. Graph between Acceleration (A) and displacement (y) is a straight line, shown below.
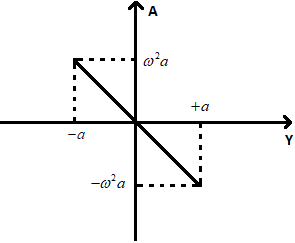
Slope of the line = – ω².
