Displacement in Simple Harmonic Motion

Displacement in Simple Harmonic Motion

(1) The displacement of a particle executing Simple Harmonic Motion at an instant is defined as the distance of particle from the mean position at that instant.

(2) Simple harmonic Motion is also defined as the projection of uniform circular motion of any diameter of circle of reference.

(3) If the projection is taken on y – axis, then from the figure:

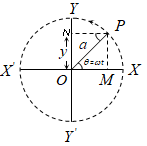
y = a sin ωt = \(a\sin \frac{2\pi }{t}\) = a sin 2πnt = a sin (ωt ± φ)

(i) y = a sin ωt, when the time is noted from the instant when the vibrating particle is at mean position.

(ii) y = a cos ωt, when the time is noted from the instant when the vibrating particle is at extreme position.

(iii) y = a sin (ωt ± φ), when the vibrating particle is φ phase leading or lagging from the mean position.

4) If the projection of P is taken on X – axis then equations of Simple Harmonic Motion can be given as: x = a cos (ωt ± φ) = \(a\cos \left( \frac{2\pi }{T}t\pm \phi  \right)\) = a cos (2πnt ± φ).

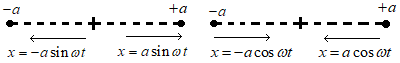
5) Direction of displacement is always away from the equilibrium position; particle is moving away from or is coming towards the equilibrium position.