When any object is moved then its speed is changed which is called velocity while the change in velocity is acceleration. When it is changed continues then it is in accelerating condition which is called the rate of acceleration. It is equal to the ratio of change in velocity with respect to time between the given paths. The vector quantity acceleration is used to show the increasing or decreasing speed or changing direction of object.
As we know that a free falling object is under the influence of gravity with an acceleration of 9.8 m/s in downward direction. The free falling objects are free from air resistance. This is the gravitational acceleration or acceleration under gravity denoted with the symbol of g with the standard value of 9.8 m/s but it is varied in different gravitational environments. Gravitational Fields widget is used for investigating the effect of location on the value of g. Let’s discuss about the calculation of acceleration due to gravitational force and its properties.
What is acceleration due to gravity?
The most common type of force is the force due to gravity. It is experienced by all of us in everyday life. For everyone, falling of an apple from its tree was a common sight and was considered as a natural phenomenon. But for Sir Isaac Newton, even though he was a boy at that time, this phenomena made him think inquisitively. Ultimately, he found that the reason of objects falling towards ground is that the Earth has an inherent property of exerting an attraction of force on the objects. This force is called force of gravity and the acceleration generated on the objects due to this force is called Acceleration due gravity.
As per the definition of force, the equation of force due to gravity is given by, W = mg.
Where,
m = mass of the Object
g = acceleration due to gravity.
In this case, the force is better known as the weight of the object. Also the acceleration in this case is the acceleration due to gravity. It is a constant and denoted by the letter g. The approximate value of acceleration due to gravity in feet is 32 ft/s² or in meters is 9.8 m/s².These are the values of acceleration of gravity on the Earth.
Acceleration due to Gravity formula: Consider an object of mass m lying on or near the surface of the Earth. Let Me be the mass of the Earth and Re be its radius i.e., Re is the distance between the object and the centre of the Earth.
According to Newton’s law of gravitation, the force of attraction (F) between the Earth and the object is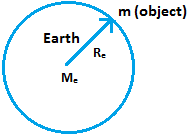
A body of mass m lying on the surface of the Earth.
\(F\,=\,\frac{G{{M}_{e}}m}{R_{e}^{2}}\) … (1)
According to Newton’s second law of motion this force produces an acceleration (g) in the object.
F = ma (∵a = g)
F = mg
\(g\,=\,\frac{F}{m}\) … (2)
Substituting the value of F in eq (2) we get,
\(g\,=\,\frac{G{{M}_{e}}m}{R_{e}^{2}\times m}\),
\(g\,=\,\frac{G{{M}_{e}}}{R_{e}^{2}}\) … (3)
From equation (3) it is very clear that acceleration due to gravity does not depend on the mass m of the object. It only depends on the mass of the Earth (Me) and the distance from the centre of the Earth to the object.
How to find the Acceleration due to gravity?
Problem: Calculate the acceleration due to gravity for a planet having mass 4 x 10²³ kg and is 3 x 10⁶ m away from the sun?
Solution: Mass of Planet, M = 4 x 10²³ kg
Radius, r = 3 x 10⁶ m
Gravitational Constant, G = 6.67 x 10̄¯¹¹ Nm²/kg²
Acceleration due to gravity, \(g\,=\,\frac{GM}{{{r}^{2}}}\)
\(=\,\frac{6.67\times {{10}^{-11}}\times 4\times {{10}^{23}}}{{{(3\times {{10}^{6}})}^{2}}}\)
= 2.964 m/sec²