Complex Numbers: The numbers of the form x +iy are known an complex numbers .here x and y real numbers and i = √-1 is iota.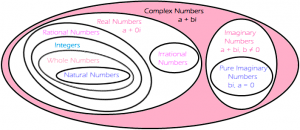
A complex number may also defines as an ordered pair of real numbers and it is denoted by symbol (x, y).
Where x is called real part and y is called imaginary part.
Set of Complex Numbers C = {x + iy: x, y ϵ R, i = √-1}.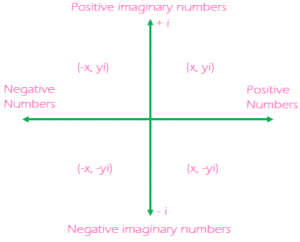
Conjugate of A Complex Numbers: Let x + iy is a complex numbers then conjugate of z is denoted by z’ and is equal to x – iy.
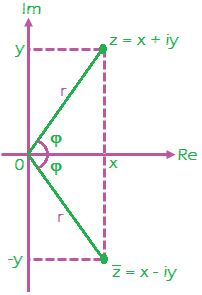Thus geometrically the conjugate of z is the reflection of point image of z in the real axis
From the definition it is clear that conjugate of a complex number can be obtained by replacing i by -i
Ex: if z = 3 + 4i, then z’ = 3 – 4i
Ex:
| Complex Number |
Complex Conjugate |
| 2 + i |
2 – i |
| – 3 + 7i |
– 3 – 7i |
| 6 – 4i |
6 + 4i |