Description of the motion for a given interval of time.
u = velocity of the particle in the beginning of the interval.
v = velocity of the particle at the end of the interval.
a = constant acceleration of the particle.
s = displacement of the particle in the given time interval
xi = co-ordinate of the particle along the line of motion, in the beginning of the interval.
xf = coordinate of the particle along the line of motion at the end of the interval.
= the time interval.
The figure, describes the position, velocity and coordinate of a particle moving along x-axis at two different time and.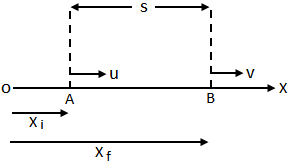
(A) By definition:
aavg = v-u/ t₂ – t₁
If acceleration of the particle is constant then
aavg = ainst = a
Hence, a = v – u/t, where, t = t₂ – t₁
(B) Displacement of the particle
s = xf – xi = <v> x t
If particle is moving with a constant acceleration then average velocity is defined as
<v> = (v + u)/2
s = (v + u)/2 x t
s = (u + at) + u/2 x t
As v = u + at from the equation
s = ut + ½ at²
(C) From equation a = (v – u)/t, t = (V – u)/a
If we put this value of t in equation s == [(V + u)/2] t we get
s = (v + u)/2 x (v – u)/a, v² = u² + 2as
Kinematical equations: The following derived equations are known as kinematical equations.
(i) v = u + at
(ii) s = ut + ½ at²
(iii) v² = u² + 2as.
Note:
(a) Any of the above equations can be used directly to solve the problems if and only if acceleration of the particle is a constant
(b) You must consider the sign of respective quantities.
Example: A particle is moving along a straight line with constant acceleration. At a point A on the line its velocity is equal to 4 m/s and at a point B its velocity becomes 6 m/s. If distance between these two points is 2 m find
(a) The acceleration of the particle
(b) The time taken by the particle to go to B from A.
(c) If at time t = 0, particle is at point A find the distance moved by the particle in the 5th seconds.
Solution:
(a) In the given situation initial velocity u = 4 m/s and final velocity v = 6 m/s displacement s = 2m
∵ v² = u² + 2as
=> a = v² – u²/2s
=> (36m²/s² – 16 m²/s²)/2x2m = 5m/s²
(b) u = 4 m/s, v = 6 m/s and a = 5 m/s².
∵ v = u + at
=> t = v –u/a = (6m/s – 4m/s)/5m/s² = 0.4s
(c) Distance moved by the particle in 5 second is
=> S5 = 4m/s x 5s + ½ x 5m/s² x 25s² = 165/2 m = 82.5 m
Distance moved by the particle in 4 s is
=> S4 = 4m/s x 4s + ½ x 5m/s² x 16s² = 56m
Distance moved in the 5th second is S = S₅ – S₄
=> S = 82.5m – 56m = 26.5m