Trigonometrical or Polar representation of Complex Numbers

Trigonometrical or Polar representation of Complex Numbers

Let z = x + iy is a complex number which is denoted by a point P (x, y) in a complex plane, then OP = |z| and ∠POX = θ = arg (Z).

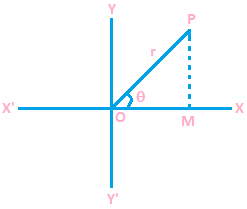
In ΔPOM,

\(\cos \theta =\frac{OM}{OP}\),

\(\cos \theta =\frac{x}{|z|}\),

Then x = |z| cosθ and θ.

\(\sin \theta =\frac{PM}{OP}\).

\(\sin \theta =\frac{y}{|z|}\).

Then y = |z| sinθ

We know that

Z = x+ iy

Z = |z| cosθ + i |z| sinθ

Z = |z| (cosθ + i sinθ)

Z = r (cosθ + i sinθ)

Where r = |z| and \(\theta ={{\tan }^{-1}}\left( \frac{y}{x} \right)\),

This form of z is known as polar form

In general, polar form is z = r [cos (2nπ + θ) + i sin (2nπ + θ)].

Where,

r = |z|, θ = arg (z) and n ϵ N.