Trends in Physical Properties of Periodic Elements

 1. Atomic Radius:

It is defined as the distance from the centre of the nucleus to the outermost shell of electrons. For practical purposes, atomic radius can be defined in many ways.

a) Covalent Radius:

1. Half of the inter-nuclear distance between two identical or almost identical atoms bonded by a single covalent bond.
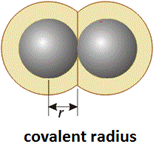
2. For a diatomic molecule,
   Distance (A – A) = radius of A + radius of A
   or d=2r_A or r_A=d/2
3. For a hetero nuclear diatomic molecule,
   Distance (A – B) = radius of A + radius of B
   The above relations hold good only when the bond is purely covalent.

b) Van der Waals’ Radius :

1. Half of the inter-nuclear distance between the nuclei of two non-bonded adjacent atoms belonging to different molecules having identical atoms in solid state.
2. This radius is taken into consideration for those cases where intermolecular attractive forces are less strong, e.g., weak dispersion forces. The examples of such molecules are molecules of noble gases, saturated molecules etc.

‘The covalent radius is always smaller than van der Waals’ radius for a given element’.

c) Crystal Radius:

1. The atomic radius of metals and inert gases in solid state is called their crystal radius
2. It is defined as half of the inter-nuclear distance between two non-bonded adjacent atoms in closed packed crystal lattice.

A crystal radius is 10 – 15 % greater than the covalent radius of a particular atom but is smaller than its van der Waals’ radius.

Trends in atomic radii:

1. Atomic radii of elements increase on moving down the group due to increase in the number of shells and increase in screening effect, which reduces effective nuclear charge.
2. Atomic radii of elements decrease while moving from left to right in a period. This is due to the fact that effective nuclear charge increases as number of inner electrons remain the same throughout the period and the change occurs only in the number of valence electrons.
3. In case of transition elements, atomic radii remains almost same because the electrons add to penultimate, i.e., (n – 1) d sub shell.
   Consequently, the increased nuclear charge is almost compensated by the screening effect.

2. Ionic Radius:

2. It’s the distance between the nucleus and the point at which nucleus exerts its influence, in an ion is called ionic radius.
3. For the determination of cationic and anionic radii, X-ray diffraction techniques are used.

a) Radii of Cation:

1. Radius of cation < radius of its neutral atom. Because of increase in the effective nuclear charge and decrease in the number of orbits for most of the cases.
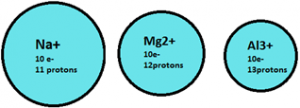
2. If various cations have same number of electrons (isoelectronic), the cation having greater number of protons is smallest in size.
3. Greater is the positive charge on the cation of a given atom, smaller is its ionic radius. E.g.,
   Fe⁺ > Fe²⁺ > Fe³⁺
   Similarly, Sn > Sn²⁺ > Sn⁴⁺

b) Radius of Anion:

1. Radius of anion > radius of its neutral atom.
2. It is due to decrease in effective nuclear charge.
3. In case of isoelectronic anions, the anion having greater number of protons is smallest in size. E.g.,

	N3-	> O2−	> F−
Number of e− :	10	10	10
Number of p :	7	8	9

4. Greater is the negative charge on an atom, greater is its radius. e.g., out of O2−, O⁻ and O the order of size is O²⁻ > O⁻ > O.

Trend in Ionic Radius:

In case of isoelectronic species, the ionic radii decrease with increase in atomic number.  In a group, the ionic radius of cation as well as anion increases on moving downwards.

3. Variation of size in inner transition elements:

1. The inner transition elements are the f – block elements.
2. The elements from La to Lu (14 elements) are called lanthanides. They are characterized by the filling up of the anti-penultimate 4f orbitals.
3. Lanthanum is the first member of the third transition series, and it has one 5d and two 6s electrons.
4. The next element is Cerium, which while still retaining two 6s electrons, has two electrons in the 4f orbitals and none in the 5d orbitals.
5. The atoms of the elements from cerium to lutetium have two to fourteen electrons in 4f- orbitals, respectively.
6. These elements constitute the first inner transition series known as lanthanides and, although lanthanum itself does not possess any 4f electrons; it is customary to include this element in this series.
7. Except for lanthanum, gadolinium and lutetium, which have single 5d electrons none of the lanthanides have electrons in 5d orbital.

 Lanthanide contraction:

1. The 4f electrons constitute inner shells and are rather ineffective in screening the nucleus; thus there is a gradual increase in the attraction of the nucleus for the peripheral electrons as the nuclear charge increases, and a consequent contraction in atomic radius is observed.
   For example: The ionic radii of the +3 cations decrease steadily from a value of 115 pm for La³⁺ to a value of 93 pm for Lu³⁺.
2. The regular decrease in atomic radii with increase in atomic number is known as lanthanide contraction.
3. The lanthanide contraction considerably influences the chemistry of the elements, which succeed the lanthanides in the periodic table.

For instance: The atomic radii of zirconium (At. No. 40) and hafnium (At. No. 72) are almost identical and the chemistry of these two elements is strikingly similar. Incidentally, the density of hafnium (which immediately follows the lanthanides) is almost twice the density of zirconium (which is in the same group).