Slope of tangent and normal: The slope of the tangent to a continuous curve y = (x) at point p(x₁, y₁) is = \({{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\).
If the tangent of curve makes an angle θ with x-axis then \(\tan \theta ={{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\).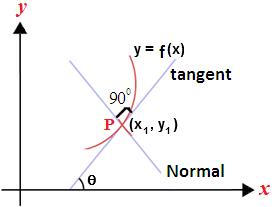
If tangent is parallel to x – axis then θ = 0.
If it is perpendicular to x-axis (i.e. parallel to y-axis) then θ = π/2.
Slope of normal at p = – \(\frac{1}{{{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}}\)= – cot θ.
Equation of tangent: Tangent to the curve y = f(x) at point (x₁, y₁) pass through P and having slope \({{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\).
∴ The equation of tangent at (x₁, y₁) to y = f(x) is y – y₁ = \({{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\) (x – x₁).
Equation of normal to y = f(x) at (x₁, y₁) is y – y₁ = \(\frac{-1}{{{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}}\) (x – x₁).
y – y₁ = – \({{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},{{y}_{1}} \right)}}\) (x – x₁).
Note:
i) If \({{\left( \frac{dy}{dx} \right)}_{p}}\) = ∞, then tangent at P (x₁, y₁) is parallel to y-axis and its equation x = x₁.
ii) If \({{\left( \frac{dy}{dx} \right)}_{p}}\) = 0, then the normal at p(x₁, y₁) is parallel to y-axis and its equation is x = x₁.
iii) The equation of tangent and normal to the curve having its parametric equation x = f(t) and y = g(t) given by y – g(t) = \(\frac{g’\left( t \right)}{f’\left( t \right)}\) (x – f(t))… Equation of Tangent.
Equation of normal is y – g(t) = – \(\frac{f’\left( t \right)}{g’\left( t \right)}\) (x – f(t)).
Angle of intersection of two curves: The angle of intersection of two curves defined to be the angle between the tangents to the two curves at their point of intersection.
Let C₁ and C₂ be two curves be 2 curves having equation y = f(x) and y = g(x) respectively. Let P, PT₁ and PT₂ tangents to the curves C₁ and C₂ respectively at common point of intersection.
Then the angle between PT₁ and PT₂ is the angle of intersection of C₁ and C₂. Let θ₁ and θ₂ be angles made PT₁ and PT₂ with positive direction of x-axis in anti-clock wise sense then m₁ = tan θ₁ = slope of tangent to y = f(x) at
P = \({{\left( \frac{dy}{dx} \right)}_{{{C}_{1}}}}\).
m₂ = tan θ₂ = slope of tangent to y = f(x) = \({{\left( \frac{dy}{dx} \right)}_{{{C}_{2}}}}\).
∴ Angle between tangents is tan θ = \(\frac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}\).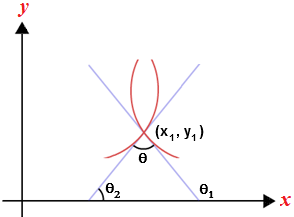
\(\tan \theta =\frac{{{\left( \frac{dy}{dx} \right)}_{{{C}_{1}}}}-{{\left( \frac{dy}{dx} \right)}_{{{C}_{2}}}}}{1+{{\left( \frac{dy}{dx} \right)}_{{{C}_{1}}}}{{\left( \frac{dy}{dx} \right)}_{{{C}_{2}}}}}\).
The other angle between the tangents is 180 – θ.
Generally the smaller of these two angles is taken to be the angle of intersection.