Superficial Expansion
When the temperature of a two – dimensional object is changed, its area changes, then the expansion is called superficial expansion. A two – dimensional object, such as a thin metallic plate, changes area when its temperature is raised or lowered.
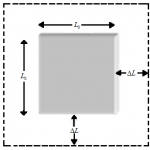
For an isotope material the area expansion may be expressed in terms of the linear expansion coefficient α.Consider a rectangular area of dimension l₁ and l₂.
The area (A₀) = l₁ x l₂.
Differentiating both sides with respect to T, we get:
\(\frac{dA}{dT}={{l}_{1}}\frac{d{{l}_{2}}}{dT}+{{l}_{2}}\frac{d{{l}_{1}}}{dT}\).
dA/ dT = l₁ (αl₂) + l₂(αl₁) = αl₁l₂ + αl₁l₂
dA/ dT = 2αl₁l₂
dA = 2αl₁l₂dT … (1)
If α is constant over the temperature range of under consideration, then equation (1) can be integrated.
\(\int\limits_{{{A}_{i}}}^{{{A}_{f}}}{dA}=2\alpha {{l}_{1}}{{l}_{2}}\int\limits_{{{T}_{i}}}^{{{T}_{f}}}{dT}\).
ΔA = 2αA₀ΔT.
Where,
A₀ = Original Area,
ΔT = Temperature Change,
ΔA = βA₀ΔT
Where,
β = Coefficient of superficial expansion, it is twice the coefficient of linear expansion α.
Final area of the plate, A = A₀ (1 + βΔT)
The average coefficient of linear expansion, β = ΔA/ A₀ΔT.
The unit of β is °C⁻¹ (or) K⁻¹. Its dimension is θ⁻¹.
