Guys ever got confused with all the equations of straight lines including different forms??
Well, here goes a simple way to understand and remember the fundamentals of straight lines.
Definition of a Straight Line: A straight line is a curve such every point on the line segment pointing any two points on it lies on it.
Note:
1) Every first degree equation in x, y represents a straight line.
When we say that a first degree equation in x, y i.e., represents a line ax + by + c = 0, it means that all points (x, y) satisfying ax + by + c = 0 lie along the line. Thus, a line is also defined as the locus of a point satisfying condition ax + by + c = 0 where a, b, c are constants.
Slope (Gradient) of a line: The trigonometric tangent of the angle that a line makes with the positive direction of the x-axis in anti-clock wise sense is called the slope (or) gradient of the line.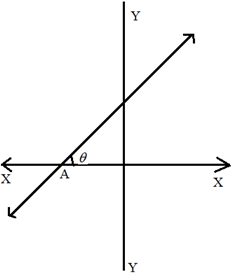
Slope of line is generally denoted by ‘m’ thus m = tanθ
Note:
1) A line parallel to x-axis makes angle 0 degrees.
2) Perpendicular to x-axis makes an angle 90 degrees with x-axis
3) The angle of inclination of a line with positive direction of x-axis in anti-clockwise sense always lies between 0 degrees and 180 degrees.
4) If m > 0 then θ is acute
If m < 0 then θ is obtuse.
Slope of a line in terms of coordinates of any two points on it: Let P (x₁, y₁) and Q (x₂, y₂) be two points on a line making an angle θ with the positive direction of x-axis then draw PL, QM perpendicular to x-axis and PN is perpendicular on QM. PN = LM = OM – OL = x₂ – x₁, QN = QM – NM = QM – PL = y₂ – y₁.
\(\tan \theta =\frac{QN}{PN}=\frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\).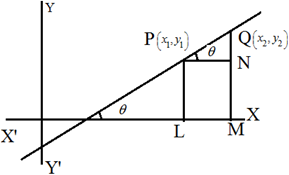
Angle between two lines: The angle θ between lines having slopes m₁ and m₂ is given by \(\tan \theta =\pm \frac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}}\).
Intercepts of a line on the axes: If a straight line cuts x-axis at A and y-axis at B. then OA and OB are known as the intercepts of the line on x-axis and y-axis respectively.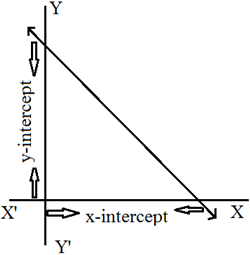
Different forms of the equation of a straight line
Slope intercept form of a line: The equation of line with slope m and making an intercept ‘c’ on y-axis is y = mx + c
Note:
If line passes through origin, c = 0
Therefore, the equation of a line passing through origin is y = mx.
Reduction of general form to slope intercept form: The general form of the equation of a line is Ax + By + C = 0.
\(y=\left( \frac{-A}{B} \right)x+\left( \frac{-C}{B} \right)\).
\(m=slope=-\frac{coeff.\,of\,x}{coeff.of\,y}\).
The point slope form of a line: The equation of a line which passes through point (x₁, y₁) and has slope m is y – y₁ = m (x -x₁).
Two point form of a line: The equation of line passing through two points A (x₁, y₁), B (x₂, y₂) is \(y-{{y}_{1}}=\left( \frac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)\).
Note: The equation of a line passing through two points (x₁, y₁) and (x₂, y₂) can also in determinant form \(\left| \begin{matrix}x & y & 1 \\{{x}_{1}} & {{y}_{1}} & 1 \\{{x}_{2}} & {{y}_{2}} & 1\\\end{matrix}\right|=0\).
Intercept form of a line: The equation of line which cuts off intercepts a and b respectively from x and y –axes is \(\frac{x}{a}+\frac{y}{b}=1\).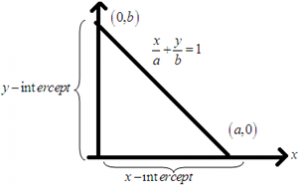
Reduction of general equation of line to intercept form: The general equation of line is Ax + By + C = 0
Ax + By = -C
\(\frac{x}{\left( \frac{-C}{A} \right)}+\frac{y}{\left( \frac{-C}{B} \right)}=1\).
Intercept on x-axis = \(\frac{-C}{A}\).
Intercept on y-axis = \(\frac{-C}{B}\).
Normal or perpendicular form of a line: The equation of straight line upon which the length of perpendicular from origin is P and this perpendicular makes an angle ‘α’ with x-axis is x cosα + y sinα = p.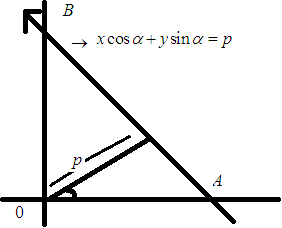
Reduction of general form of line to the normal form: Ax + By + C = 0 is \(\left( \frac{A}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)x+\left( \frac{B}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)y=\left( -\frac{C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)\) is normal form with
\(\cos \alpha =\frac{A}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\).
\(sin\alpha =\frac{B}{\sqrt{{{A}^{2}}+{{B}^{2}}}}\).
\(P=\left( \frac{-C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right)\).
Straight line: Symmetric form: (or) Distance form of a line: The equation of line passing through (x₁, y₁) and making angle with positive direction of x-axis is \(\frac{x-{{x}_{1}}}{\cos \theta }=\frac{y-{{y}_{1}}}{\sin \theta }=r\).
Where ‘r’ is distance of point (x, y) on the line from the point (x₁, y₁).
Note: Co-ordinates of any point on the line at a distance ‘r’ from the given point (x₁, y₁) is (x₁ + r cosθ, y₁ + r sinθ) or (x₁ – r cosθ, y₁ – r sinθ).