Equation of parabola in its standard form: Let S be focus and ZZ’ be directrix of a parabola. Draw SK perpendicular from S on directrix and bisect SK at A
⇒ AS = SK
Where A lies on parabola
SK = 2a
⇒ SA = SK = a
Let choose A be origin, AS as X – axis and AY line perpendicular AS as Y – axis.
Then co – ordinates S = (a, 0) and equation of directrix is x + a = 0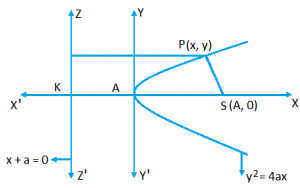
P lies on parabola SP = PM
SP² = PM²
⇒ (x – a)² + (y – 0)² = (x + a)²
⇒ y² + x² – 2ax + a² = x² + a² + 2ax
⇒ y² = 4ax
y² = 4ax is the standard equation of parabola
Tracing of parabola: We have y² = 4ax, a > 0
The equation can be written as y = k ± 2 √ (ax) we observe
- Symmetry: For every value of x there are two equal and opposite values of y.
- Region: For negative value of x then y value is imaginary.
∴ No part of curve lies to left of y-axis. - Origin: The curve passes through origin and tangent at origin is x=0 that is y – axis.
- Intersection with axis: The curve meets.
- Co – ordinate axis: The curve meets the co – ordinates axis only at origin.
- Portions occupied: As x → ∞, y → ∞.
∴ Curve extends to infinity, to the right of y – axis
Various results related to parabola:
Double ordinate: let P be any point on parabola y² = 4ax. A chord passing through P perpendicular to axis of the parabola is called the double ordinate through point P.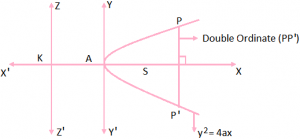
Latus rectum: A double ordinate through focus is called the latus rectum.
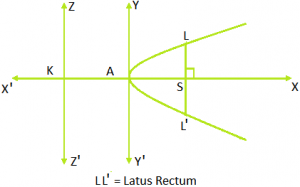Length of latus rectum = 4a
Co – ordinates of < and <’ are (a, 2a) and (a, -2a) respectively
Focal distant at any point: The distant P(x, y) from the focus S is called the focal distance of the point P
Now,
\(SP=\sqrt{{{\left( x-a \right)}^{2}}+{{y}^{2}}}\) \(=\sqrt{{{\left( x-a \right)}^{2}}+4ax}\left[ \because P\left( x,y \right)lies\,on\,parabola \right]\) \(=\sqrt{{{\left( x+a \right)}^{2}}}\)⇒ SP = a + x
∴ a + x is the focal distance of point P(x, y)