Relative Velocity

Generally we consider the reference as earth (i.e., stationary) and we will mention the velocities of all the bodies. So it will be relative earth as earth velocity will be “O” its original velocity will be equal to the relative velocity w.r.t earth.

But in the relative velocity concept we will speak about the velocity of one body with respect to the other moving body.

Relativity concept in scalar:

Let the age of A → 40 years

Let the age of B → 20 years

Then the age of “A” relative to B is 20.

Age of A – age of B i.e., 40 – 20 = 20

The age of “B” relative to A is “- 20”

Age of B – age of A = 20 – 40 = – 20

As the “age” is scalar we can straight away subtract them but when we comes to vector for “ex”

Let the velocity of “A” be 20 m/s along +ve x axis and the velocity of “B” be 20 m/sc along +ve y – axis. Then relative velocity of A w.r.t B is V_A – V_B

Relative velocity of B w.r.t A is V_B – V_A

From the parallel to green law of vectors. We get,

|V_A – V_B| = √ (V_A² + V_B² + 2V_A + V_B cosθ)

θ is the angle between V_A and V_B

|V_A – V_B| = √ (V_A² + V_B² + 2V_A + V_B cos90)

|V_A – V_B| = √ (V_A² – V_B²)

Direction of resultant = tan⁻¹ [(b sinθ)/ (a – b cosθ)]

(i) Relative motion of a boat in a river: Let v_ω be the velocity of water in a river flowing in the direction RQ and v_b be the velocity of the boar in still water is shown in figure. The resultant velocity of the boat in the river is given by v = √ (v_ω² + v_b² + 2 v_ωv_b cosθ)

a) To cross the river of width d along the shortest path which is PQ, the boat must move along PR making an angle (90⁰ + θ) with the direction of the stream such that the direction of the resultant velocity v is along PQ. Angle θ is given by sin θ = v_ω/v_bAlso v = √ (v_b² + v_ω²)

The time taken to cross the river along the shortest path is given by t = d/v = d/ √ (v_b² – v_ω²)

b) To cross the river in the shortest time, the boat should move along PQ. The shortest time is given by t = d/v_b. At this time, the boat will reach the point R on the opposite bank of the river at a distance x from the point Q. From the Figure, we have x = d tan θ, but tan θ = v_ω / v_b. Therefore, x = d (v_ω/ v_b)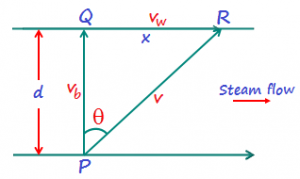(ii) Holding an Umbrella to Protect from Rain: let v_r be the velocity of the rain falling vertically downward and v_m the velocity of a man walking from north to south direction. In order to protect himself from rain, the must hold his umbrella in the direction of the resultant velocity v, which is given by v = √ (v_r² + v_m²).

This is the speed with which the rain strikes the umbrella. If θ is the angle subtended by the resultant velocity v with the vertical, then from triangle ORM`, we have tan θ = RM’/ OR = v_m/v_r or θ = tan⁻¹ (v_m/ v_r)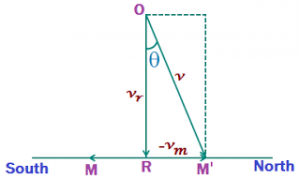Thus the man must hold the umbrella at an angle θ with the vertical towards south.

Example: A jet airplane travelling at the speed of 500 km h⁻¹ ejects its products of combustion at the speed of 1500 km h⁻¹ relative to the jet plane. What is the speed of the latter with respect to an observer on the ground?

Solution:

\({{\overrightarrow{V}}_{jg}}\)→ Velocity of jet w.r. to ground = 500î

\({{\overrightarrow{V}}_{cj}}\)Velocity of combustion w.r. to jet = 1500î

\({{\overrightarrow{V}}_{cg}}={{\overrightarrow{V}}_{cj}}-{{\overrightarrow{V}}_{cg}}\)

1500î = V_cg +500î

\({{\overrightarrow{V}}_{cg}}\) = 1500 î – 500 î

\({{\overrightarrow{V}}_{cg}}\) = 1000î

\({{\overrightarrow{V}}_{cg}}\) = 1000km/h