Refrigerator (Or) Heat Pump
A refrigerator of heat pump is basically a heat engine run in reverse direction. It essentially consists of three parts:
1) Source: At higher temperature \({{T}_{1}}\).
2) Working Substance: It is called refrigerant liquid ammonia and freon works as working substance.
3) Sink: At lower temperature \({{T}_{2}}\).
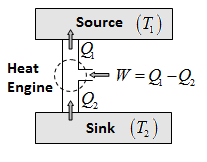
The working substance takes heat \({{Q}_{2}}\) from a sink at lower temperature, as a net amount of work done W on it by an external agent and gives out a larger amount of heat \({{Q}_{1}}\) to a hot body at temperature \({{T}_{1}}\). Thus, it transfers heat from a cold to a hot body at the expense of mechanical energy supplied to it by an external agent. The cold body is thus cooled more and more. The performance of a refrigerator is expressed by means of coefficient of performance \(\beta \) which is defined as the ratio of the extracted from the cold body to the work needed to transfer it to the hot body.
\(\beta =\frac{Heat\,\,Extracted}{Work\,\,Done}=\frac{{{Q}_{2}}}{W}=\frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}\)A perfect refrigerator is one which transfer heat from cold to hot body without doing work i.e. W = 0, so that \({{Q}_{1}}={{Q}_{2}}\) and hence \(\beta =\infty \).
Carnot Refrigerator:
For Carnot refrigerator, \(\frac{{{Q}_{1}}}{{{Q}_{2}}}=\frac{{{T}_{1}}}{{{T}_{2}}}\) \(\Rightarrow \frac{{{Q}_{1}}-{{Q}_{2}}}{{{Q}_{2}}}=\frac{{{T}_{1}}-{{T}_{2}}}{{{T}_{2}}}\) (or) \(\Rightarrow \frac{{{Q}_{2}}}{{{Q}_{1}}-{{Q}_{2}}}=\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\) . So, coefficient of performance, \(\beta =\frac{{{T}_{2}}}{{{T}_{1}}-{{T}_{2}}}\). Where, \({{T}_{1}}=\) Temperature of surrounding, \({{T}_{2}}=\) Temperature of cold body. It is clear that \(\beta =0\) when \({{T}_{2}}=0\). i.e. the coefficient of performance will be zero if the cold body is at the temperature equal to absolute zero.
