Properties of Focal Chord – II

Properties of Focal Chord – II

Example 4: Semi-latus rectum is the harmonic mean of SP and SQ, where P and Q are the extremities of focal chord.

Solution: PQ is the focal chord

\(SP=a+a{{t}^{2}}\) and \(SQ=a+\frac{a}{{{t}^{2}}}\).

\(\frac{1}{SP}+\frac{1}{SQ}=\frac{1}{a+a{{t}^{2}}}+\frac{1}{a+a/{{t}^{2}}}=\frac{1}{a}\).

 \(2a=\frac{2SP\times SQ}{SP+SQ}\).

Example 5: Circle described on the focal length as diameter touches the tangent at the vertex.

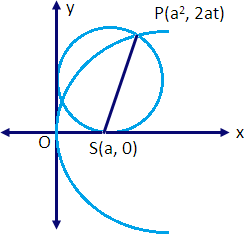
Solution: The equation of the circle described on SP as diameter is (x-at²) (x-a) + (y-2at) (y-0) = 0

Solving it with the y-axis, x = 0, we have (0-at²)(0-a) + (y-2at)(y-0) = 0

y² – 2aty + a²t² = 0

Which has equal roots

Hence, the y-axis touches the circle

Also, the point of contact is (0, at).

Example 6: Circle described on the focal chord as diameter touches the directrix.

Solution: The equation of the circle described on PQ as diameter is \(\left( x-a{{t}^{2}} \right)\left( x-\frac{a}{{{t}^{2}}} \right)+\left( y-2at \right)\left( y+\frac{2a}{t} \right)=0\).

Solving it with x = -a, we have

\(\left( -a-a{{t}^{2}} \right)\left( -a-\frac{a}{{{t}^{2}}} \right)+\left( y-2at \right)\left( y+\frac{2a}{t} \right)=0\).

\({{y}^{2}}-2a\left( t-\frac{1}{t} \right)y+{{a}^{2}}\left( t-\frac{1}{t} \right)=0\).

Which is a perfect square

Hence, x = -a touches the circle.