Parabola – Conormal Points and Pair of Tangent

Parabola – Conormal Points and Pair of Tangent

Conormal Points: The points on the parabola through which normal drawn are concurrent i.e., pass through the same point are called conormal points. The conormal points are also called the feet of the normal. Points A, B, C in which the three normal from P (h, k) meet the parabola are called conormal points.

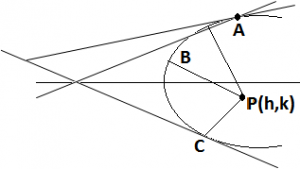
Results on Conormal Points:

(i) The algebraic sum of the slopes of the normal at conormal points to zero.

(ii) The sum of the ordinates of the conormal points is zero.

(iii) The centroid of the triangle formed by the conormal points on a parabola lies on its axis.

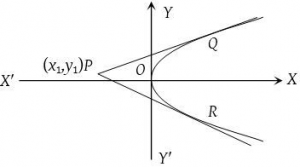
Pair of Tangents: Let P (x₁, y₁) be any points outside the parabola S = y² – 4ax then the equation of the pair of tangents drawn from the point P to the parabola is given by

SS₁ = T²

Where,

S = y² – 4ax,

S₁ = y₁² – 4ax₁ and

T = yy₁ – 2a (x + x₁)

Problems: If the point P (1, 4) is outside of parabola y² + 4y = 3x, then equation of pair of tangent

Solution: Given that

y² + 4y = 3x and the point P (1, 4)

We know that the equation of pair of tangent is SS₁ = T²

T = y₁y + 4/ 2 (y₁ + y) – 3/ 2 (x + x₁) at point P (1, 4)

T = 4y + 2 (4 + y) – 3/ 2 (x + 1)

= 6y – 3x/ 2 + 13/ 2x

= 1/2 (12y – 3x + 13)

S = y² + 4y – 3x at point

S₁ = (4)² + 4 (4) – 3 (1)

= 29

equation of pair of tangent is SS₁ = T²

(y² + 4y – 3x) (29) = 1/4 (12y – 3x + 13) ²

29(y² + 4y – 3x) = 1/4 (12y – 3x + 13)²