Orbital Velocity of Satellite

Satellites are natural or artificial bodied describing orbit around a planet under its gravitational attraction. Moon is a natural satellite while INSAT – 1B is an artificial satellite of earth. Condition for establishment of artificial satellite is that the center of orbit of satellite must coincide with center or earth or satellite must move around great circle of earth. Orbital velocity of a satellite is the velocity required to put the satellite into its orbit around the earth.

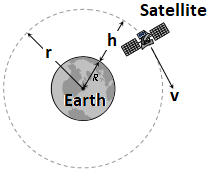
For revolution of satellite around the earth, the gravitational pull provides the required centripetal force.

\(\frac{m{{v}^{2}}}{r}=\frac{GMm}{{{r}^{2}}}\).

\(v=\sqrt{\frac{GM}{r}}=\sqrt{\frac{g{{R}^{2}}}{R+h}}=R\sqrt{\frac{g}{R+h}}\) (∵ GM = gR²; r = R + h)

\(v=R\sqrt{\frac{g}{R+h}}\).

Orbital velocity is independent of the mass of the orbiting body and is always along the tangent of the orbit. i.e.., satellites of different masses have same orbital velocity, if they are in the same orbit.

Orbital velocity depends on the mass of central body and radius of orbit and the orbital velocity of the satellite when it revolves very close to the surface of the planet and for a given planet, greater the radius of orbit, lesser will be the orbital velocity of the satellite.