Consider a closed conducting loop ABCD, with the arm CD sliding, placed in a horizontal plane. Let B be a uniform magnetic field perpendicular to the plane of the loop and directed into it. Let the conductor CD be moved towards right with a velocity v as shown in Fig. As the conductor CD slides, the area of the closed loop changes from ABCD to ABEF, during a small interval of time dt.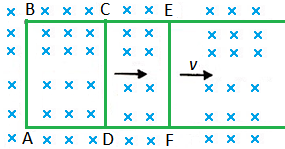
The change in flux passing through the closed loop dφ.
= Flux density B x Change in area
= B x (area ABEF – ABCD)
= B x area DCEF
= B x CD x DF = Bl x vdt
Where l is the length of the conductor CD in the magnetic field.
Induced e.m.f = – \(\frac{d\phi }{dt}\) , the magnitude of the induced e.m.f. = E = \(\frac{d\phi }{dt}\) = Blv.
The e.m.f. induced due to the motion of the conductor in a uniform magnetic field is called the motional e.m.f. It depends upon
(i) The magnetic flux density B;
(ii) The length of the conductor l in the magnetic field;
(iii) The speed v with which the conductor is moved in the magnetic field.
If the conductor is inclined at an angle θ with the direction of B then the magnitude of the induced emf = Blv sinθ.
The direction of the induced e.m.f. is given by Lenz’s law or Fleming’s right hand rule. If R is the resistance of the whole circuit then the magnitude of the induced current,
\(I=\frac{E}{R}=\frac{Blv}{R}\)