Guys..!! Here’s a very quick way to learn about monotonic functions, their properties, to find the maxima, minima and their properties etc.
Monotonic function: A function f(x) is said to be monotonic on an interval (a, b) if it is either increasing or decreasing (a, b)
Definition 1: A function f(x) is said to be increasing (decreasing) at a point x₀ containing, if there is an interval (x₀ – h, x₀ + h) such that f(x) is increasing (decreasing) on (x₀ – h, x₀ + h).
Definition 2: A function f(x) is said to be increasing (decreasing) on [a, b] if it is increasing (decreasing) on (a, b) and it is also increasing (decreasing) on [a, b] and it is also increasing (decreasing) at x = a and x = b.
Necessary and sufficient condition Montonicity of functions:
Necessary condition: Let f(x) be a differentiable function defined on (a, b) then f’(x) > 0 or f’(x) < 0 according as f(x) is increasing or decreasing on (a, b)
If f(x) is an increasing function on (a, b) then tangent at every point on curve y = f(x) makes an acute angle in the +ve direction of x-axis.
\(\tan \theta >0\Rightarrow \frac{dy}{dx}>0\) or f’(x) > 0 ” x ϵ (a, b).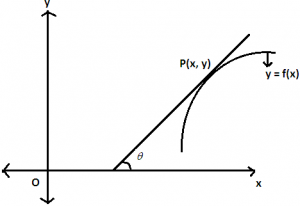
Similarly for decreasing function on (a, b) then the tangent at every point on the curve
y = f(x) makes obtuse angle θ with direction of x – axis.
\(\tan \theta <0\Rightarrow \frac{dy}{dx}<0\) or f’(x) < 0 ” x ϵ (a, b).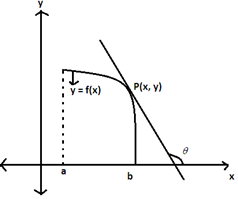
Sufficient condition: Let f be a differentiable real function defined on open interval (a, b)
a) If f’(x) > 0 ” x ϵ (a, b), then f is increasing on (a, b)
b) If f’(x) < 0 ” x ϵ (a, b), then f is decreasing on (a, b)
Properties of Monotonic functions:
i) If f(x) is strictly increasing function on an interval [a, b] then fˉ¹exists and also a strictly increasing function
ii) If f(x) is strictly increasing function on an interval [a, b] such that it is continuous then fˉ¹is continuous on [f(a), f(b)]
iii) If f(x) is continuous on [a, b] such that f’(c) ≥ 0 (f’(c) < 0) ” x ϵ (a, b) then f(x) is monotonically (strictly increasing function on [a, b])
Maxima and Minima:
Maxima: Let f(x) be function with domain D Ì R then f(x) is said to attain the maximum value at a point a ϵ D if f(x) ≤ f(a) “ x ϵ D. A is called the point of maximum f(a) is known as Maximum value of f(x).
Minimum: Let f(x) be a function with Domain D Ì R. Then f(x) is said to attain the minimum value at a point a ϵ D if f(x) ≥ f(a) ” x ϵ D. The point a is called the point minimum f(a) is known as Minimum value of f(x).
Local Maxima: A function f(x) is said to attain a local maximum at x = a if $ a neighborhood (a – δ, a + δ) of a such that f(x) < f(a) ” x ϵ (a – δ + a + δ) x ≠ a.
In such a case f(a) is called the local maximum value of f(x) at x =a
Local maximum value of f(x) at x = 0
Local minima: A function f(x) is said to attain a local minimum at x = a if $ a neighborhood (a – δ, a + δ) of a such that f(x) > f(a) ” x ϵ (a – δ + a + δ) x ≠ a then f(a) is called local minima of f(x) at x = a.
The points at which a function attains either the local maximum values or local minimum values are known as extreme points and both local maximum and minimum values are called the extreme values of f(x) at the extreme points of f(x).
Note:- By a local maximum or (Minimum) values of a function at a point x = a mean the greatest or (the least) value in the nbd of point x = a and not the absolute minimum . In fact a function may have any number of points of local maximum or (local minimum)
A necessary condition for f(a) to be an extreme value of function is that f’(a) = 0 in case it exist.
Points of inflection: A point of inflection is a point at which a curve is changing concave upwards to concave downwards (or) vice – versa. A curve y = F(x) has one of its points fn(c) = 0 and fn (c) ≠ 0 changes sign as x is increases through x = C.
An arc y = f(x) is called concave downward if, at each of the points the arc lies below the tangent.
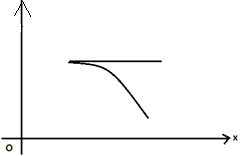f”(x) < 0 for concave downward curve
f”(x) > 0 for concave upwards curve
Properties of maxima and minima
I) If f(x) is continuous function in its domain, the at least one maxima and one minima must lies. Between two equal values of x.
II) Maxima and Minima Occur alternatively, between two maxima there is one minimum and vice-versa
III) If f’(x) → ∞, x → a or b f’(x) = 0 for any one value of x between a and b then f(c) is necessarily the minimum and the least value f(x) → ∞, x → a or b then f(c) is necessarily the maximum.
Maximum and minimum values of f(x) in closed interval: Let y = f(x) be function defined on
Steps:
1) Find \(\frac{dy}{dx}=f'(x)\).
2) Put f’(x) =0 and find values of x let c₁, c₂, c₃ … cn be values of x
3) Take the maximum and minimum out of the values F(a), f(c₁), f(c₂) … f(cn), f(b).
Therefore, the maximum and minimum values are absolute maximum or minimum values of the function.