Moment of Inertia of a Triangular Lamina about its Base
Inertia is a property of a body to resist the change in linear state of motion. It is measured by the mass of the body. The moment of inertia (I) of a body is a measure of its ability to resist change in its rotational state of motion.
Consider a triangular lamina of base (b), altitude (h) and mass (M). Surface mass density is mass per unit area of the lamina.
\(\sigma =\frac{M}{\left( \frac{1}{2}bh \right)}=\frac{2M}{bh}\).
Consider a rectangular differential strip parallel to the base of width (dy), at a distance (y) from the axis of rotation:
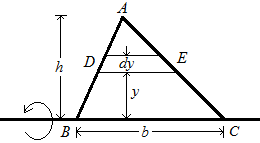
From similar triangles ΔADE and ΔABC, we have:
\(\frac{DE}{BC}=\frac{h-y}{h}\).
\(DE=(h-y)\frac{b}{h}\).
Area of strip DE, \(dA=(h-y)\frac{b}{h}dy\).
Moment of Inertia of the strip DE about the axis of rotation BC is given by:
dIBC = (Mass of strip DE) (Distance from axis)².
\(d{{I}_{BC}}=\left( \frac{2M}{bh}(h-y)\frac{b}{h}dy \right){{y}^{2}}\).
\(d{{I}_{BC}}=\frac{2M}{{{h}^{2}}}{{y}^{2}}(h-y)dy\).
Integrate the above expression between the limits from y = 0 to y = h.
\({{I}_{BC}}=\int\limits_{0}^{h}{\frac{2M}{{{h}^{2}}}}(h{{y}^{2}}-{{y}^{3}})dy=\frac{2M}{{{h}^{2}}}\left[ \left( \frac{h{{y}^{3}}}{3} \right)-\left( \frac{{{y}^{4}}}{4} \right) \right]_{0}^{h}=\frac{M{{h}^{2}}}{6}\).
\({{I}_{BC}}=\frac{M{{h}^{2}}}{6}\).
Therefore, the Moment of Inertia of a Triangular Lamina about its base \(\left( {{I}_{BC}} \right)=\frac{M{{h}^{2}}}{6}\).
