Modulus of Rigidity
The modulus of rigidity is also known as shear modulus. It is the material property with a value equal to the shear stress divided by the shear strain. It can be used to explain how a material resists transverse deformation but this is practical for small deformations only.
What is Modulus of Rigidity (Shear Modulus)?
Modulus of Rigidity is the coefficient of elasticity for a shearing force. It is defined as the ratio of shear stress to the shear strain. It can be experimentally determined from the slop of a stress – strain curve created during tensile tests conducted on a sample of the material.
Formula to find the Modulus of Rigidity: When we applied shear load on an object, the linear dimensions of the objects remain same but the shape of the body deform. The strain associated with the shear stress in known as shear strain. The ratio of shear stress to shear strain is known as modulus of Rigidity.
Shear Stress = Shearing Force/ Area under Shear = F/A.
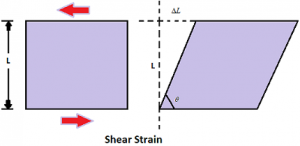
Shear Strain = Relative displacement of any layer/ Its distance from a fixed layer.
Shear Strain = tan θ = θ = ΔL/ L.
Modulus of Rigidity (G) = Shear Stress/ Shear Strain = [(F/A)]/ [(ΔL/L)]
Modulus of Rigidity (G) = FL/ AΔL.
Where,
G is the Shear Modulus of a body expressed in N/m².
How to find the Modulus of Rigidity?
Problem: Find the shear modulus, if the stress experienced by a body is 5 x 10⁴ N/m² and strain is 4 x 10⁻²?
Solution:
Stress = 5 x 10⁴ N/m².
Strain = 4 x 10⁻²
Shear Modulus (G) = Shear Modulus (G) = Shear Stress/ Shear Strain = 5 x 10⁴ N/m²/ 4 x 10⁻².
∴ Shear Modulus (G) = 1.25 x 10⁶ N/m².
