Ideal Gas Equation
To know the property of gasses we need to have a standard gas, but which gas should it be? Helium, Oxygen, Nitrogen, Hydrogen, Carbon dioxide and there are thousands of other gasses we have to learn, but our scientists have found that no matter what gas we study, if we take one mole sample of that gas and put it in the same container and maintain a constant temperature, the pressure is almost same and at lower densities even those small differences in the measurement also disappear. Thus, at low densities, all the real gasses tend to obey one universal law, the law is described by an equation known as the Ideal Gas Equation.
What is Ideal Gas Equation?
Ideal gases are gases that obey gas laws like Boyle law, Charles Law and Avogadro Law over all temperature and pressures. By combining Boyle’s and Charles’ laws, an equation can be derived that gives the overall relationship between pressure, temperature and the volume of the gas. This is known as combined Ideal Gas Equation.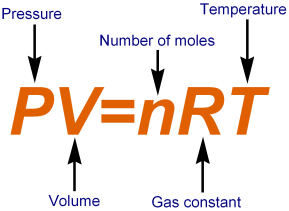
Derivation of Ideal Gas Equation: According to Boyle’s law, for a given gas at constant temperature the volume is inversely proportional to pressure of gas.
\(V\,\,\,\,\propto \,\,\,\,\frac{1}{P}\,\,\) … (1) (Constant T)
According to Charles’ law,
\(V\,\,\propto \,\,\,T\,\) … (2) (Constant P)
Combining equation (1) and (2):
\(V\,\,\,\,\propto \,\,\,\,\frac{T}{P}\)
\(\Rightarrow \,\,\,\,V\,\,\,=\,\,\,K\,\,\,\frac{T}{P}\)
\(\Rightarrow \,\,\frac{PV}{T}\,\,\,=\,\,\,K\,\,\,=\) Constant.
Now for two gases at two different temperature, pressure and volume.
\(\frac{{{P}_{1}}\,{{V}_{1}}}{{{T}_{1}}}\,\,\,=\,\,\,\frac{{{P}_{2}}\,\,{{V}_{2}}}{{{T}_{2}}}\,\,\,=\) Constant.
The above relationship is very useful for converting the volume of a gas from one set of conditions to another.
The constant is related with quantity of gas or number of moles of gas. Hence, \(K\,\,\propto \,\,n\)
\(\Rightarrow \,\,\,K\,\,=\,\,n\,R\)
Where, R is the universal gas constant. The value of ‘R’ is same for all gases.
However the value of R will change with pressure, volume and temperature of gas. Therefore the Ideal gas Equation is derived as
\(\frac{PV}{T}\,=\,n\,R\)
\(\Rightarrow \,\,\,P\,V\,=\,n\,R\,T\)
For one mole (n = 1),
\(PV\,=\,RT\)
The word ‘ideal’ is used here because in reality no gas obeys the above condition and the gases, which deviate from ideal behaviour are called as real gases.
How to find the Ideal Gas Equation?
Problem: Calculate the number of moles of hydrogen (H2) present in a 500cm3 sample of hydrogen gas at a pressure of 760 mm of Hg and 27 0C?
Solution: Given,
Volume, (V) = 500 cm3
Pressure, (P) = 760 mm of Hg = \(\frac{760}{760}\,=\,1\,atm\)
Temperature, (T) = 27 0C = 27 + 273 = 300 K
Universal Gas Constant, (R) = \(82.1\,c{{m}^{3}}.atm/K.mole\)
Number of moles, (n) = ?
Using Ideal Gas Equation:
PV = nRT
\(\Rightarrow \,\,\,n\,\,=\,\,\frac{P\,V}{R\,T}\)
\(\Rightarrow \,\,n\,\,\,\,=\,\,\,\,\frac{(1\,\,\,atm)\,\,\,\times \,\,\,(500\,\,\,c{{m}^{3}})}{(82.1\,\,\,atm\,.\,c{{m}^{3}}/K\,.\,mole)\,\,\,\times \,\,(300\,\,\,K)}\,\,=\,\,0.0203\,moles\,=\,2.03\,\times \,{{10}^{-2}}\,moles.\)
Therefore, Number of moles is \(2.03\,\times \,{{10}^{-2}}\,moles.\)