Rocket Propulsion
When ordinary vehicles, such as automobiles and locomotives, are propelled, the driving force for the motion is friction. In the case of the automobile, the driving force is the force exerted by the road on the car. A locomotive “pushes” against the tracks, hence, the driving force is the force exerted by the tracks on the locomotive. However, a rockets moving in space has no road or track to push against. Therefore, the source of the propulsion of a rocket must be something other than friction. Therefore, the source of the propulsion of a rocket must be something other than friction.
The operation of a rocket depends upon the laws of conservation of linear momentum as applied to a system of particles, where the system is the rocket plus its ejected fuel.
Rocket propulsion can be understood by first considering the mechanical system consisting of a machine gun mounted on a cart on wheels. As the gun is fired, each bullet receives a momentum mv in some direction. Where, v is measured with respect to a stationary earth frame. The momentum of the system made up of cart, gun and bullets must be conserved. Hence, for each bullet fired, the gun and the cart must receive a compensating momentum in the opposite direction. That is, the reaction force exerted by the bullet on the gun accelerates the cart and gun, and the cart moves in the direction opposite that of the bullets. If n is the number of bullets fired each second, then the average force exerted on the gun is Favg = nmv in a similar manner, as rocket moves in free space, its linear momentum changes when some of its mass is released in the form of ejected gases. Because the gases are given momentum when they are ejected out of the engine, the rocket receives a compensating momentum in the opposite direction. Therefore, the rocket is accelerated as a result of “Push”, or “Thrust”, from the exhaust gases. In free space, the centre of mass of the system moves uniformly, independent of the propulsion process.
Suppose that at some time t, the magnitude of the momentum of a rocket plus its fuel is (M + Δm), where, v is the speed of the rocket relative to the Earth (figure. (a)). Over a short time interval Δt, the rocket ejects fuel of mass Δm and so at the end of this interval the rockets speed is v + Δv, where, Δv is the change in speed of the rocket (figure. (b)). If the fuel is ejected with a speed ve relative to the rocket, the velocity of the fuel relative to a stationary frame of reference is v – ve. Thus, if we equate the total momentum of the system to the total final momentum, we obtain, (M + Δm)v = M (v + Δv) + Δm (v – ve).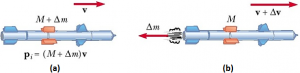
Where,
M represents the mass of the rocket and its remaining fuel after an amount of fuel having mass Δm has been ejected. Simplifying this expression gives, M Δv = ve Δm.
We also could have arrived at this result by considering the system in the centre- of-mass frame of reference, which is a frame having the same velocity as the centre of mass of the system. In this frame, the total momentum of the system is zero. Therefore, if the rocket gains a momentum MΔv by ejecting some fuel, the exhausted fuel obtains a momentum ve Δm in the opposite direction, so that MΔv – veΔm = 0 … (1)
If we now take the limit as Δt goes to zero, we get Δt → dv and Δm → dm
Furthermore, the increase in the exhaust mass dm corresponds to an equal decrease in the rocket mass, so that dm = – dM. Note that dM is given a negative sign because it represents a decrease in mass. Using this fact, we obtain Mdv = ve and dm = – ve dM.
Integrating this equation and taking the initial mass of the rocket plus fuel to be Mi and the final mass of the rocket plus its remaining fuel to be Mf, we obtain
\(\int\limits_{{{v}_{i}}}^{{{v}_{f}}}{\,\,dv}\,\,=\,\,\,\,-\,\,\,{{v}_{e}}\,\,\int\limits_{{{M}_{i}}}^{{{M}_{f}}}{\frac{dM}{M}}\),
\({{v}_{f}}\,\,\,-\,\,\,{{v}_{i}}\,\,\,=\,\,\,{{v}_{e}}\,\,\ln \,\left( \frac{{{M}_{i}}}{{{M}_{f}}} \right)\).
This is the basic expression of rocket propulsion. First, it tells us that the increase in rocket speed is proportional to the exhaust speed of the ejected gases ve. Therefore, the exhaust speed should be very high. Second, the increase in rocket speed is proportional to the natural logarithm of the ratio Mi/ Mf. Therefore, this ratio should be as large as possible, which means that the mass of the rocket without its fuel should be as small as possible and the rocket should carry as much fuel as possible.
The thrust on the rocket is the force exerted on it by the ejected exhaust gases. We can obtain an expression for the thrust from Equation 9.40.
\(Thrust\,\,\,=\,\,\,M\frac{dv}{dt}\,\,\,=\,\,\,\left| {{v}_{e}}\,\,\frac{dM}{dt} \right|\),
This expression shows us that the thrust increases as the exhaust speed increases and as the rate of change of mass (called the burn rate) increases.