Hyperbola – Theorems

Hyperbola – Theorems

Theorem Statement: The equation of the chord joining the two points A(x₁, y₁), B(x₂, y₂) on the hyperbola S = 0 is S₁ + S₂ = S₁₂

Theorem: The difference of the focal distance of any point on the hyperbola is constant i.e., if P is appointed on the hyperbola \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\) with foci S and S’ then |PS’ – PS| = 2a

Proof: Let e be the eccentricity and L = 0, L’ = 0 be the directrices of the hyperbola. Let C be the center and A, A’ be the Vertices of the hyperbola

∴ AA’ = 2a

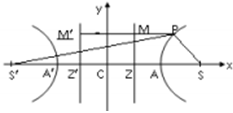
Foci of the hyperbola are S (ae, 0), S (-ae, 0)

Let p (x₁, y₁) be a point on the hyperbola

Let M, M’ be the projection of P on the directrices L = 0, L‘ = 0 respectively

\(\frac{SP}{PM}=e\)

\(\frac{SP’}{PM’}=e\)

Let Z, Z’ be the points of intersection of transverse axis with directrices

∴ MM’ = ZZ’ = CZ + CZ’ = 2a/e

PS’ – PS = e PM’ – e PM = e(PM’ – PM)

= e(MM’) = e(2a/e) = 2a

Example: Find the equation to the hyperbola and transverse axis who foci are (4, 2) and (8, 2) and eccentricity is 2.

Solution: Foci are S (4, 2) and S’ (8, 2) and eccentricity (e) = 2

Centre C = the mid point of the foci

 \(=\left( \frac{4+8}{2},\frac{2+2}{2} \right)\)

\(\left( \frac{12}{2},\frac{4}{2} \right)=\left( 6,2 \right)\)

SS’ = 2ae = 8 – 4 = 4

ae = 2

Given e = 2

a (2) = 2

a = 1

b² = a² (e² – 1)

= 1(4 – 1) = 3

Equation of hyperbola is \(\frac{{{(x-h)}^{2}}}{{{a}^{2}}}-\frac{{{(y-k)}^{2}}}{{{b}^{2}}}=1\).`

\(\frac{{{(x-6)}^{2}}}{1}-\frac{{{(y-2)}^{2}}}{3}=1\).

And transverse axis of hyperbola

2a = 2(1) = 2.