Heating Curve
If to a given mass (m) of a solid, heat is supplied at constant rate P and a graph is plotted between temperature and time, the graph is as shown in figure and is called heating curve. From this curve it is clear that:
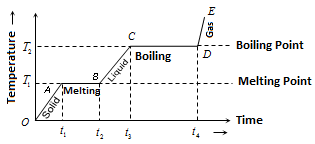
1) In the region OA temperature of solid is changing with time so, Q = mc, ΔT ⇒ PΔt = mc, ΔT [as Q = PΔt].
But as (ΔT/ Δt) is the slope of temperature – time curve, cs α 1/ (Slope of line OA) i.e. specific heat is inversely proportional to the slope of temperature – time curve.
2) In the region of AB temperature is constant, so it represents change of state, i.e. melting of solid with melting point T1. At A melting starts and at B all solid is converted into liquid. So, between A and B substance is partly solid and partly liquid. If LF is the latent heat of fusion. Q = mLF (or) LF = P (t₂ – t₁)/ m[as Q = P (t₂ – t₁) ⇒ LF α Length of line AB.
i.e. Latent hear of fusion is proportional to the length of line of zero slope, in this region Specific heat α 1/tan 0 = ∞.
3) In this region BC temperature of liquid increases so specific heat of liquid will be inversely proportional to the slope of line BC. i.e., c₁ α 1/ (Slope of line BC).
4) In the region CD temperature is constant, so it represents the change of state, i.e., boiling with boiling point T₂. At C all substance is in liquid state while at D in vapor state and between C and D partly liquid and partly gas. The length of line CD is proportional to latent heat of vaporization.
i.e. LV α Length of line CD, in this region-specific heat α 1/tan 0 = ∞.
5) The line DE represents gaseous state of substance with its temperature increasing linearly with time. The reciprocal of slope of line will be proportional to specific heat or thermal capacity of substance in vapor state.
