Consider a circuit containing an inductance L and a resistance R connected in series with a d.c. source of steady e.nif E volt and a tap key K (Morse key). When the key is pressed K is in contact with the point A, the current grows from zero to a maximum value of I₀. Let the current in the circuit at any instant t be I.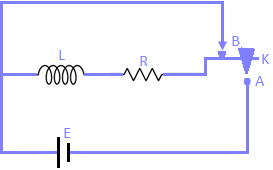 As the current increases, the magnetic field surrounding the inductor increases. The flux passing through the inductor changes and an e.m.f. is induced in it. This e.m.f. opposes the growth of current through the inductor. So the e.m.f. is called back e.m.f. and is equal to – L dl/dt. The negative sign shows that induced e.m.f. opposes theapplied e.m.f. E. The net e.m.f. in the circuit is E – L. dl/dt.
As the current increases, the magnetic field surrounding the inductor increases. The flux passing through the inductor changes and an e.m.f. is induced in it. This e.m.f. opposes the growth of current through the inductor. So the e.m.f. is called back e.m.f. and is equal to – L dl/dt. The negative sign shows that induced e.m.f. opposes theapplied e.m.f. E. The net e.m.f. in the circuit is E – L. dl/dt.
The resultant potential difference across the resistance R, according to Kirchhoff’s voltage law is,
IR = E – L dl/dt
L dl/dt + IR = E
This is the equation for the e.m.f. of a circuit containing an inductance L and a resistance R in series. When the current grows to a steady maximum value I₀, dI = 0, hence E = I₀R.
\(L\frac{dI}{dt}+~IR={{I}_{0}}R\), \(L\frac{dI}{dt}=~\left( {{I}_{0}}-~I \right)R\), \(\frac{dI}{{{I}_{0}}-I}=\frac{R}{L}~dt\)
Integrating, log (I₀ – I) = (- R/L) t + K
Where K is the constant of integration. When t = 0, I = 0. Substituting in equation (ii)
log I₀ = K
\({{\log }_{e}}\left( {{I}_{0}}-I \right)=~-\frac{R}{L}t+\log {{I}_{0}},{{\log }_{e}}\left( \frac{{{I}_{0}}-I}{{{I}_{0}}} \right)=~-\frac{R}{L}t\).
\(\frac{{{I}_{0}}-I}{{{I}_{0}}}={{e}^{\frac{-Rt}{L}}},~1-\frac{I}{{{I}_{0}}}={{e}^{\frac{-Rt}{L}}},~1-{{e}^{\frac{-Rt}{L}}}=\frac{1}{{{I}_{0}}}\).
I = I – 0 [1 – e-Rt/L]
I is the current flowing through the L-R series circuit at any instant t and I₀ is the maximum value of the current. The equation for the growth of current through an L – R circuit, when it is connected to d.c source of esn.f. This equation is called Helmholtz, equation.
The growth of current is exponential. With increase in time t, e-Rt/L approaches zero and the current approaches the final steady value I₀.
i.e. when t = ∞ (infinity), I = I₀ (1 – e– ∞) = I₀. This means the current reaches its maximum value after infinite time. But in practice the current reaches its maximum value (approximately) after a short time depending on the value of L and R.
Time Constant:
It can be seen that LIR has the dimensions of time. L/R is called the inductive time constant or the time constant of an L-R circuit.
Time constant = L/R = λ
When = L/R,
\(I={{I}_{0}}\left( 1-{{e}^{-\frac{R}{L}*\frac{L}{R}}} \right)={{I}_{0}}\left( 1-{{e}^{-1}} \right)={{I}_{0}}\left( I-\frac{I}{e} \right)\).
\(I={{I}_{0}}~\left( 1-\frac{1}{2.71782} \right)={{I}_{0}}~\left( 1-0.36794 \right)={{I}_{0}}*0.6321\).
Hence time constant of an L-R circuit may be defined as the time taken by the current to grow from zero to 0.63214 I₀ or 63.2% of its final steady value.
