Force on Surface Immersed in a Liquid and Centre of Force
Consider a rectangular plane surface of area A held vertically in a static liquid of density ρ. Let, top and bottom edges of the plane surface be at vertical depths of h₁ and h₂ respectively below the free surface of the liquid. The pressure intensity at the top edge is P₁ = ρgh₁. The pressure intensity at the bottom edge is P₂ = ρgh₂. As the pressure intensity increases linearly from ρgh₁ to ρgh₂, so the average pressure intensity over the entire surface is:
\({{P}_{avg}}=\frac{{{P}_{1}}+{{P}_{2}}}{2}=\rho g\left( \frac{{{h}_{1}}+{{h}_{2}}}{2} \right)\).
\({{P}_{avg}}=\rho g\left( \frac{{{h}_{1}}+{{h}_{2}}}{2} \right)\) … (1)
Thus, the net force on the vertical surface is:
F = Pavg x Area of the surface
Now, Substitute equations (1) in the above equation, we get:
\(F=\rho g\left( \frac{{{h}_{1}}+{{h}_{2}}}{2} \right)\times A\).
This result can be generated for a surface of any shape. Let us analyse the same case by another approach. It is easy to see that the trust due to the liquid on any surface can be obtained as:
Thrust = Area x Hydrostatic pressure at the centroid of the area.
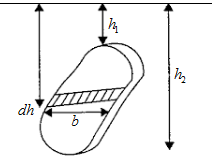
Consider a plane surface of any arbitrary shape, immersed in a liquid of density ρ. Let us sub divide the area into infinitesimally thin horizontal strips. Consider one such strips of width (b) and thickness dh, at a depth h below the free liquid surface. Normal thrust on this strip is:
dF = Pressure x Area = ρgh (bdh)
Total thrust exerted by the liquid on the area is F = ΣdF = Σρghbdh = \(\rho g\sum\limits_{h={{h}_{1}}}^{{{h}_{2}}}{bhdh}\).
Now, if h̅ be the depth of the centroid of the area, below the free surface and A is the total area, then
\(\overline{h}=\sum\limits_{h={{h}_{1}}}^{{{h}_{2}}}{\frac{(bdh)h}{A}}\).
\(A\overline{h}=\sum\limits_{h={{h}_{1}}}^{{{h}_{2}}}{(bdh)h}\).
∴ F = (ρgh̅) A
Hence, the force on a vertical immersed surface is the product of the pressure on the centroid of the surface and the area of the surface.
