Equation of a Plane Passing Through the Line of Intersection of Two Planes
Let π₁ and π₂ be two planes with equations \(\vec{r}.{{\hat{n}}_{1}}={{d}_{1}}\) and \(\vec{r}.{{\hat{n}}_{2}}={{d}_{2}}\), respectively. The position vector of any point on the line of intersection must satisfy both the equation.
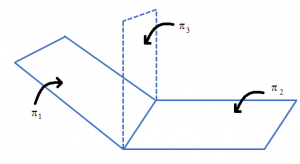
If \(\vec{t}\) is the position vector of a point on the line, then
\(\vec{t}.{{\hat{n}}_{1}}={{d}_{1}}\) and \(\vec{t}.{{\hat{n}}_{2}}={{d}_{2}}\).
Therefore, for all real values of λ, we have
\(\vec{t}.\left( {{{\hat{n}}}_{1}}+\lambda {{{\hat{n}}}_{2}} \right)={{d}_{1}}+\lambda {{d}_{2}}\)… (1)
Since \(\vec{t}\) is arbitrary, it satisfies for any point on the line.
Hence, the equation \(\vec{r}.\left( {{{\hat{n}}}_{1}}+\lambda {{{\hat{n}}}_{2}} \right)={{d}_{1}}+\lambda {{d}_{2}}\) represents a plane π₃ which is such that if any vector satisfies both the equation π₁ and π₂, it also satisfies the equation π₃.
Cartesian Form: In cartesian system, let \({{\vec{n}}_{1}}={{A}_{1}}\hat{i}+{{B}_{1}}\hat{j}+{{C}_{1}}\hat{k}\), \({{\vec{n}}_{2}}={{A}_{2}}\hat{i}+{{B}_{2}}\hat{j}+{{C}_{2}}\hat{k}\) and \(\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\).
Then (1) becomes
\(x\left( {{A}{1}}+{{A}{2}}\lambda \right)+y\left(
{{B}{1}}+{{B}{2}}\lambda \right)+z\left( {{C}{1}}+{{C}{2}}\lambda \right)={{d}{1}}+\lambda {{d}{2}}\),
\(\left( {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z-{{d}_{1}} \right)+\lambda \left( {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z-{{d}_{2}} \right)=0\).
Which is the required Cartesian form of the equation of the plane passing through the intersection of the given planes for each value of λ.
Example: Find the equation of a plane containing the line of intersection of the plane x + y+ z – 6 = 0 and 2x + 3y + 4z + 5 = 0 and passing through (1, 1, 1).
Solution: The equation of plane passing through the line of intersection of the given planes is
(x + y + z – 6) + λ (2x + 3y + 4z + 5) = 0 . . . (1)
If it is passes through (1, 1, 1),
(1 + 1 + 1 – 6) + λ (2.1 + 3.1 + 4.1 + 5) = 0
-3 + λ (14) = 0
λ = 3/14
λ value substitute in equation (1)
(x + y + z – 6) + (3/14) (2x + 3y + 4z + 5) = 0
Required equation is 20x + 23y + 26z – 69 = 0.
