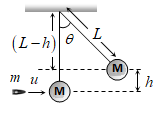
Collision between Bullet and Vertically suspended block

A collision is said to have taken place if two bodies interact with each other and undergo a change in momentum and or kinetic energy. A bullet of mass m is fired horizontally with velocity u in block of mass M suspended by vertical thread. After the collision bullet gets embedded in block. Let the combined system raised up to height h and the string makes an angle θ with the vertical.

(i) Velocity of System: Let v be the velocity of the system just after the collision.

Now, Momentum_Bullet + Momentum_Block = Momentum_{(Bullet+Block)}

mu + 0 = (m + M) v \(\Rightarrow \,\,v=\frac{mu}{\left( m+M \right)}\) … (1)

(ii) Velocity of Bullet: Due to energy which remains in the bullet – block system, just after the collision, the system rises up to height h. By the conservation of mechanical energy:

½ (m + M) v² = (m + M) gh \(\Rightarrow v=\sqrt{2gh}\),

Now, substituting the above value in the equation (1), we get: \(\sqrt{2gh}=\frac{mu}{\left( m+M \right)}\),

\(\Rightarrow u=\left[ \frac{\left( m+M \right)\sqrt{2gh}}{m} \right]\).

(iii) Loss in Kinetic Energy: We know that the formula for loss kinetic energy in perfectly inelastic collision.

\(\Delta K.E=\frac{1}{2}\left( \frac{{{m}_{1}}{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}} \right){{\left( {{u}_{1}}-{{u}_{2}} \right)}^{2}}\) (When bodies are moving in same direction)

∴ \(\Delta K.E=\frac{1}{2}\left( \frac{mM}{m+M} \right){{\left( u \right)}^{2}}\) (As u₁ = u, u₂ = 0, m₁ = m, m₂ = M)

(iv) Angle of string from the vertical: From the expression of velocity of bullet, \(u=\left[ \frac{(m+M)\sqrt{2gh}}{m} \right]\), we can get: \(h=\frac{{{u}^{2}}}{2g}{{\left( \frac{m}{m+M} \right)}^{2}}\).

From the figure, \(\cos \theta =\frac{\left( L-h \right)}{L}=1-\frac{h}{L}=1-\frac{{{u}^{2}}}{2gL}{{\left( \frac{m}{m+M} \right)}^{2}}\) \(\Rightarrow \,\,\theta ={{\cos }^{-1}}\left[ 1-\frac{1}{2gL}{{\left( \frac{mu}{m+M} \right)}^{2}} \right]\).