Energy stored in a Charged Capacitor

Energy stored in a Charged Capacitor

Work has to be done to transfer charges onto a conductor, against the force of repulsion from the already existing charges on it. This work is stored as a potential energy of the electric field of the conductor.

Suppose a conductor of capacity C is to be charged up to a potential V₀ and let q₀ be the final charge on the conductor. Let the potential of the conductor when thecharge on it was q (< q₀) be V = q/ C.

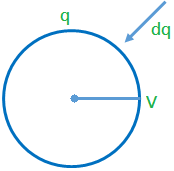
Now, work done in bringing a small charge dq at this potential is dW = V (dq) = (q/ C) dq.

Therefore, the total work done in charging it from 0 to q₀ is \(W=\int\limits_{0}^{{{q}_{0}}}{dW}=\int\limits_{0}^{{{q}_{0}}}{\frac{q}{C}dq=\frac{1}{2}\frac{{{q}_{0}}^{2}}{C}}\).

This work is stored as the potential energy, i.e., U = ½ (q²₀)/ C.

Further, by using q₀ = CV₀, we can write this expression as U = ½ CV²₀ = ½ q₀ V₀.

Potential energy of a spherical capacitor made of a single sphere is \(U=\frac{{{q}^{2}}}{2C}=\frac{{{q}^{2}}}{8\pi{{\varepsilon }_{0}}R}\) (∵ C = 4πε₀ R).

Potential energy of a spherical capacitor \(\left( U \right)=\frac{{{q}^{2}}}{8\pi {{\varepsilon}_{0}}R}\).