Electric Field due to Infinite Wire

Electric Field due to Infinite Wire

The force felt by a unit positive charge or test charge when its kept near a charge is called Electric Field. It is also defined as the region which attracts or repels a charge. The electric field is a vector quantity and it is denoted by E. the standard units of the electric field is N/C.

Consider an infinitely long wire with linear charge density λ and length L. To calculate electric filed, we assume a cylindrical Gaussian surface due to the symmetry of wire. As the electric field E is radial in direction, flux through the end of the cylindrical surface will be zero, as electric field and area vector are perpendicular to each other. The only flowing electric flux will be through the curved Gaussian surface. As the electric field is perpendicular to every point of the curved surface, its magnitude will be constant.

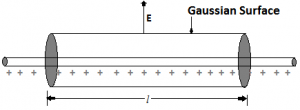
The surface area of the curved cylindrical surface is 2πrl. The electric flux through the curve is φ = E x 2πrl.

According to Gauss’s Law:

\(\phi \,\,=\,\,\frac{q}{{{\varepsilon }_{0}}}\).

\(E\times 2\pi rl\,\,=\,\,\frac{\lambda \times l}{{{\varepsilon }_{0}}}\).

\(E\,\,=\,\,\frac{\lambda }{2\pi rl}\).

In vector form, the above relation is:

\(\overrightarrow{E}\,\,=\,\,\frac{\lambda }{2\pi {{\varepsilon }_{0}}r}\widehat{n}\).

Where, \(\widehat{n}\) is radial unit vector pointing the direction of electric field \(\overrightarrow{E}\). The direction of electric field is radially outward if linear charge density is positive. On the other hand, it will be radially inward of the linear charge density is negative.