Applications of Gauss’s Law
According to Gauss’s law, the total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity. The electric flux through a closed surface is zero. If no charge is enclosed by the surface.
\({{\phi }_{E}}\,\,=\,\,\frac{{{Q}_{enclosed}}}{{{\varepsilon }_{0}}}\).
Or
\({{\phi }_{E}}\,\,=\,\,\int\limits_{s}{\overrightarrow{E}}.\overrightarrow{da}\).
So,
\({{\phi }_{E}}\,\,=\,\,\int\limits_{s}{\overrightarrow{E}}.\overrightarrow{da}\,\,=\,\,\frac{{{Q}_{enclosed}}}{{{\varepsilon }_{0}}}\).
Here, \(E\) is the total number of electric lines of force crossing through the given area, \(\phi \) is the flux associated with the charge, \(Q\) is the net charge enclosed by the closed surface, and \({{\varepsilon }_{0}}\) is the permeability of free space. Gauss’s law describes how charges create electric fields.
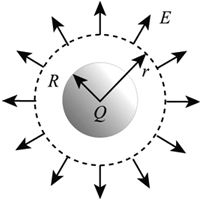
Calculate the flux associated with a uniformly charged spherical shell.
\(\phi \,\,=\,\,\oint{E.ds}\,\,=\,\,E\left( 4\pi {{r}^{2}} \right)\).
Applying Gauss’s law to find the electric field at a point located at a distance r outside the sphere.
\(E(4\pi {{r}^{2}})\,\,=\,\,\frac{Q}{{{\varepsilon }_{0}}}\).
\(Electric\,\,Field(E)\,\,=\,\,\frac{Q}{4\pi {{r}^{2}}{{\varepsilon }_{0}}}\).
