Electric Field Due to an Isolated Point Charge

Electric Field Due to an Isolated Point Charge

Electric Field is a force produce by a charge near its surroundings. This force is exerted on other charges when brought in the vicinity of this field. The SI unit of Electric field is N/C. Electric field due to a charge at a point is the force that a unit positive charge would experience if placed at that point.

Consider a point charge Q placed at the origin O. To find the electric intensity at a point P, distant r from O, place a test charge q₀ at P. According to coulomb’s law, the force exerted on q₀ by Q is:

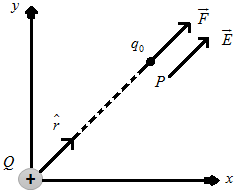
\(\overrightarrow{F}={{k}_{e}}\frac{Q{{q}_{0}}}{{{r}^{2}}}\widehat{r}\); Where, 

\(\widehat{r}\) = Unit vector from O to P, i.e. from Q to q₀.

If \(\overrightarrow{E}\) is the electric field created by Q at P, then by definition:

\(\overrightarrow{E}=\underset{{{q}_{0}}\to0}{\mathop{\lim }}\,\frac{\overrightarrow{F}}{{{q}_{0}}}=\underset{{{q}_{0}}\to0}{\mathop{\lim }}\,\frac{{{k}_{e}}\frac{Q{{q}_{0}}}{{{r}^{2}}}\widehat{r}}{{{q}_{0}}}\).

\(\overrightarrow{E}={{k}_{e}}\frac{Q}{{{r}^{2}}}\widehat{r}=\frac{1}{4\pi{{\varepsilon }_{0}}}\frac{Q}{{{r}^{2}}}\widehat{r}=\frac{1}{4\pi{{\varepsilon }_{0}}}\frac{Q}{{{r}^{3}}}\overrightarrow{r}\).

∴ \(\overrightarrow{E}=\frac{1}{4\pi{{\varepsilon }_{0}}}\frac{Q}{{{r}^{3}}}\overrightarrow{r}\).

If Q is positive, \(\overrightarrow{E}\) is directed radially outward from it and if Q is negative, \(\overrightarrow{E}\) is directed toward it. In magnitude:

\(E={{k}_{e}}\frac{Q}{{{r}^{2}}}=\frac{1}{4\pi{{\varepsilon }_{0}}}\frac{Q}{{{r}^{2}}}\).