The locus of the mid-points of a system of parallel chords of a conic is known as its diameter.
Equation of diameter of a parabola:
Let y = mx + c be a system of parallel chords of the parabola y² = 4ax.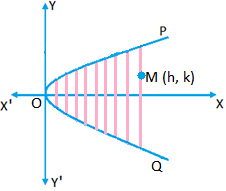
Here, m is a constant and c is a variable.
The line y = mx + c meets the parabola y² = 4ax in the points say P and Q whose ordinates (say y₁ and y₂) are the roots of the equation
∴ \({{y}^{2}}\,=\,4a\left( \frac{y-c}{m} \right)\)
⇒ my² – 4ay + 4ac = 0
∴ y₁ + y₂ = 4a/m
Let M (h, k) be the mid-points of PQ. Then,
\(k\,=\,\frac{{{y}_{1}}+{{y}_{2}}}{2}\)⇒ k = 2a/m
Hence, the locus of (h, k) is y = 2a/m