Derivative at a Point

Derivative at a Point

Let f(x)  be a differentiable function on [a, b] then corresponding to each point c ϵ [a, b] we obtain a unique real number equal to the derivative f’(c ) of f(x) at x = c This correspondence between the points in  and derivatives at their points defines a new real valued function with domain [a, b] and range a subset of R, set of real numbers, such that the image of x in [a, b] is the value of the derivative of at x i.e., Df(x)  or \(\frac{d}{dx}\left( f\left( x \right) \right)\).

Thus \(\frac{d}{dx}\left( f\left( x \right) \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( x+h \right)-f\left( x \right)}{h}\) or \(\frac{d}{dx}\left( f\left( x \right) \right)=\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( x-h \right)-f\left( x \right)}{-h}\).

The differentiation or derivative of a function it is also called the differential coefficient of f(x) but we shall be using the words differentiation or derivatives only.

Geometrical Meaning of Derivative at a Point: Consider the curve y = f(x). Let f(x) be differentiable at x = c. Let P(c, f(c)) be a point on the curve and let Q(x, f(x)) be a neighboring point on the curve. Then,

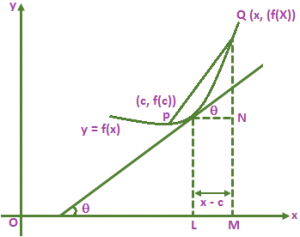
Slope of the chord PQ = \(\frac{f\left( x \right)-f\left( c \right)}{x-c}\).

Taking limit as Q → P i.e., x → c,

We get

\(\underset{Q\to P}{\mathop{\lim }}\,\)(slope of the chord PQ) = \(\underset{x\to c}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\) … (1)

As Q → P, Chord PQ becomes tangent at P. Therefore, from (1) we have

Slope of the tangent at p = \(\underset{x\to c}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\),

= \({{\left[ \frac{df\left( x \right)}{dx} \right]}_{x=c}}\) or f’(c).

Thus, the derivative of a function at a point x = c gives the slope of the tangent to the curve y = f(x) at the point (c, f(c) is a corner point of the curve y = f(x) i.e., the curve suddenly changes its direction at point P(c, f(c)).