Common Chord of Two Circles

Common Chord of Two Circles

The common chord joining the point of intersection of the two given circles is called their common chord.

If S = 0 and S’ = 0 are two intersecting circles, the equation of their common chord is S – S’ = 0

Let S = x² + y² + 2gx + 2fy + c = 0 and S’ = x₁² + y₁² + 2g’x+ 2f’y + c’ = 0 be two circles intersecting at P and Q.

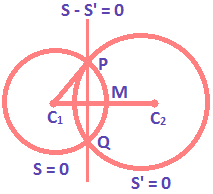
Then PQ is their common chord.

Therefore S – s’ = 0

x² + y² + 2gx + 2fy + c – (x₁² + y₁² + 2g’x + 2f’y + c’) = 0

2 (g – g’) x + 2 (f – f’) + (c – c’) = 0

This is the common chord of the two circles S = 0 and S’ = 0.

Length of the CommonChord:

PQ = 2 (PM) = \(2\sqrt{{{({{C}_{1}}P)}^{2}}-{{({{C}_{1}}M)}^{2}}}\).

Where C₁P is the radius of the circle S = 0 and C₁M is the length of perpendicular from C₁ on the common chord PQ.