Circle – General Equation
Definition: A circle is the locus of a point which moves in a plane such that its distance from a fixed point in plane is always a constant. The fixed point is called the center and the constant distance is called the radius of the circle.
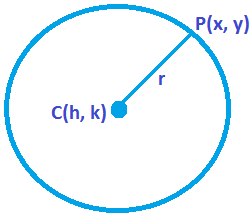
Equation of Circle (h, k) and Radius r:
The equation of circle is
(x-h)² + (y-k)² = r² …(i)
In particular, if the center is at the origin the equation of circle is
x² + y² = r²
General Equation of a Circle:The general equation of the circle
x² + y² + 2gx + 2fy + c = 0 …..(ii)
Where g, f and c are constants
To find the center and radius, (ii) can be written as
(x + g)² + (y + f)² = (√(g² +f²-c) ²
Comparing with the equation of circle given in (i), we get
h = -g, k = -f
and r = √(g² +f²-c)
therefore, the coordinates of the center are (-g, -f) and radius is √(g² +f²-c) , ( since g² +f² ≥ c)
Example: Find the equation of the circle with radius 5 whose center lies on the x – axis and passes through the point (2, 3).
Solution:Since the radius of the circle is 5 and its center lies on the x- axis,
the equation of the circle is (x – h)² + y² = 25.
It is given that the circle passes through the point (2, 3)
Therefore,
(x – h)² + y² = 25
(2 – h)² + 3² = 25
(2 – h)² = 25 – 9
(2 – h)² = 16
(2-h) = ± 4
If 2-h = 4, then h =-2
If 2-h = -4, then h = 6
Therefore, the equation of circle is
(x + 2)² + y² = 25
(or) (x-6)² + y² = 25.
Hence x² + y² + 4x – 21 = 0
(or)
x² + y² -12x + 11 = 0.