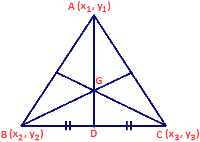
Pair of Straight Lines – Theorem
Pair of Straight Lines – Theorem Combined Equation of Pair of Lines joining Origin and the Point of Intersection of a Curve and A Line Let us find the equation of the straight line joining the origin and the Points of intersection of the curve ax² + 2hxy + by² + 2gx + 2fy + Read more about Pair of Straight Lines – Theorem[…]