Pair of Straight Lines – Theorem
Combined Equation of Pair of Lines joining Origin and the Point of Intersection of a Curve and A Line
Let us find the equation of the straight line joining the origin and the Points of intersection of the curve
ax² + 2hxy + by² + 2gx + 2fy + c = 0 … (1)
and the line
lx + my + n = 0 … (ii)
equation (ii) can be written as
lx + my + n = 0 ⇒ lx + my = -n
\(\frac{lx+my}{-n}=1\) … (iii)
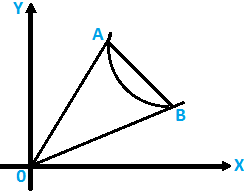
Let A and B be the points of intersection of (ii) and (i).
In the order to make (i) homogeneous with the help of (iii), we write (i) as
ax² + 2hxy + by² + (2gx + 2fy)1 + c (1) ² = 0
\(a{{x}^{2}}+2hxy+b{{y}^{2}}+(2gx+2fy)\times \left( \frac{lx+my}{-n} \right)+c{{\left( \frac{lx+my}{-n} \right)}^{2}}=0\) … (iv)
Since the coordinates of A and B satisfy (i) and (ii), these satisfy (iv) which is formed by combining (i) and (ii).
Thus, (iv) is a locus through points A and B.
Also, (iv) being a homogeneous equation of second degree in x and y represents two straight lines through the origin.
Hence, (iii) is the joint equation of OA and OB.
Example: Prove that the straight lines joining the origin to the points of intersection of the straight line hx + ky = 2hk and the curve (x – h)² + (y – k)² = c² are perpendicular to each other if h² + k² = c².
Solution: Given that,
(x – h)² + (y – k)² = c²
hx + ky = 2hk
x² + y² – 2(xh + yk) + (h² + k² – c²) = 0
x² + y² – 2(xh + yk) (1) + (h² + k² – c²) (1)² = 0 … (1)
hx + ky = 2hk
⇒ (hx + ky)/2hk = 1 … (2)
Equation (2) substitute in equation (1)
x² + y² – 2(xh + yk) ((hx + ky)/ 2hk) + (h² + k² – c²) ((hx + ky)/ 2hk)² = 0
This is the equation of the pair of lines joining the origin to the points of intersection of the given line and the curve. These will be perpendicular to each other if.
Coefficient of x² + coefficient of y² = 0
i.e., (h² + k²) (h² + k² – c²) = 0
h² + k² = c² (∵ h² + k² ≠ 0).
