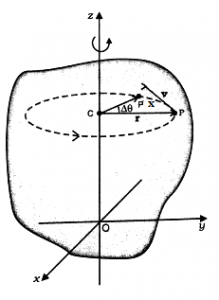
Typical particle (at a point P) of the rigid body rotating about a fixed axis (taken as the z – axis). The particle describes a circle with a centre C on the axis. The radius of the circle is r, the perpendicular distance of the point P from the axis. We also show the linear velocity vector v of the particle at P. it is along the tangent at P to the circle.
Let P’ be the position of the particle after an interval of time Δt. The angle PCP’ describes the angular displacement Δθof the particle in time Δt the average angular velocity of the particle over the interval Δt is \(\frac{\text{ }\!\!\Delta\!\!\text{ }\theta }{\text{ }\!\!\Delta\!\!\text{ }t}\). As Δt tends to zero (i.e., takes smaller and smaller values), the ratio \(\frac{\text{ }\!\!\Delta\!\!\text{ }\theta }{\text{ }\!\!\Delta\!\!\text{ }t}\) approaches a limit which is the instantaneous angular velocity \(\frac{\text{d}\theta }{dt}\) of the particle at the position P. we denote the instantaneous angular velocity by ω(the Greek letter omega). We know from our study of circular motion that the magnitude of linear velocity of a particle moving in a circle is related to the angular velocity of the particle ωby the simple relation.
v = ωr.
Where r is the radius of the circle.
We observe that at any given instant the relation v = ωr applies to all particles of the rigid body. Thus for a particle at a perpendicular distance rt from the fixed axis, the linear velocity at a given instant vt is given by
vt = ωrt.
The index i runs from 1 to n where n is the total number of particles of the body.
For particles on the axis r = 0 and hence v = ωr = 0. Thus, particles on the axis are stationary. This verifies that the axis is fixed. Note that we use the same angular velocity ω for all the particles. We therefore, refer to ω as the angular velocity of the whole body