Angular Acceleration

Angular Acceleration

Angular Acceleration is the rate change of angular velocity of a body is called angular acceleration. It is the change in velocity of moving object in respect to time. The angular acceleration is also known as rotational acceleration. It is an expression of the change in angular velocity per unit time.

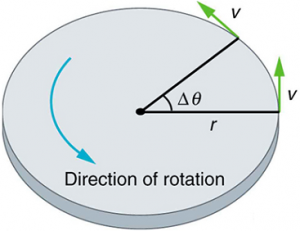
The acceleration vector and magnitude or the length is directly proportional to the rate of change in angular velocity.

Angular Acceleration Formula: The rate of change of angular velocity regarding time is angular acceleration, which is a vector quantity. It is denoted by α. The angular acceleration formula is given by

\(\omega \,\,=\,\,\frac{\theta }{t}\).

Where,

ω = Angular Velocity

θ = Angle Rotated

t = Time Taken

When the angular velocity is constant, the angular acceleration is 0. If the velocity is not constant, then the constant angular acceleration α is defined as

\(\alpha \,\,=\,\,\frac{\omega }{t}\,\,=\,\,\frac{\theta }{{{t}^{2}}}\).

If the angular acceleration is not constant and differs time to time, then

\({{\alpha }_{avg}}\,\,=\,\,\frac{({{\omega }_{2}}\,-\,{{\omega }_{1}})}{({{t}_{2}}\,-\,{{t}_{1}})}\),

And

\(Angular\,\,Acceleration\,\,(\alpha )\,\,=\,\,\frac{d\omega }{dt}\,\,=\,\,\frac{{{d}^{2}}\theta }{d{{t}^{2}}}\).

The Earth takes 23 hours and 56 minutes to complete one revolution and rotates at angular velocity of 7.2921159 x 10⁻⁵ radians/ second.