Accuracy, Precision and Error Measurement
Why do we need measurement? Measurement is the foundation for all experimental science and technology. Science is the study of nature and we need to use what we see in nature in our calculations. Today we know that the acceleration due to gravity is 9.8 m/s2 but would we be able to comprehend that if we had no means of measurement. Due to presence of universal SI units, we can exchange information with anyone since these units are used worldwide. Measurement is essential for us to understand the external world and through the millions of years of life, we all have developed a sense of measurement. You unconsciously know how much time has passed or how much distance you have walked. The problem here is that the result of every measurement by any measuring instrument contains some uncertainty. This uncertainty is referred to as Error. Here, there are two terms that are often confused with each other but are not the same, Accuracy and Precision.
What is Accuracy and Precision?
Accuracy refers to the closeness of a measured value to the actual value of the object being measured. For example, if in lab you obtain a weight measurement of 3.2 kg for a given substance, but the actual or known weight is 10 kg, then your measurement is not accurate.
Precision refers to the closeness of two or more measurements to each other. Using the example above, if you weigh a given substance five times, and get 3.2 kg each time, then your measurement is very precise. Precision is independent of accuracy. The below example will tell you about how you can be precise but not accurate and vice versa.
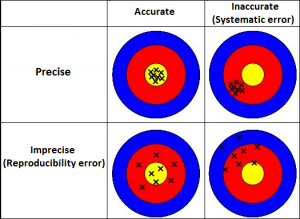
This classic diagram illustrates what combinations of accuracy and precision exist. The precise measurements both exhibit tight grouping near some portion of the dartboard. The accurate measurements are near the centre.
To determine if a value is accurate compare it to the accepted value. As these values can be anything a concept called percent error has been developed. Find the difference (subtract) between the accepted value and the experimental value, then divide by the accepted value.
% error = (accepted – experimental)/ accepted *100%
To determine if a value is precise find the average of your data, then subtract each measurement from it. This gives you a table of deviations. Then average the deviations. This will give you a value called uncertainty. A plus or minus value that says how precise a measurement is.
Deviation = (average – actual)
Standard deviation = (deviations for all measurements added together)/ number of measurements.
Errors in measurement: While measuring any physical quantity, it is impossible in principle to find its true value.
The difference between measured and the true values of a physical quantity is called the error of measurement.
Following are the various types of errors:
Systematic Errors: The errors which occur only in one direction are called Systematic Errors. The direction may be positive or negative but not be both at the same time. Systematic error is also known as a Repetitive Error as it occurs because of default machines and incorrect experiment apparatus. These errors take place if the device which is used to take measurements is wrongly calibrated. Some sources of systematic errors are as follows:
Instrumental Errors: The errors which occur due to lack of accuracy in an instrument are called instrumental errors. Instrumental Error occurs due to following reasons:
- If the instrument is not properly designed and is not accurate
- The calibration of the instrument is incorrect
- If the scale is worn off at edges or broken from somewhere
- If an instrument is giving a wrong reading instead of actual one
Examples:
- If the markings of a thermometer are improperly calibrated, let’s say it’s 108°C instead of 100°C, then it is called An InstrumentalError
- If a meter scale is worn off at its end
- If pressure of atmosphere is 1 bar and the instrument is showing 1.5 bars, then it’s again an instrumental error
- In a Vernier calliper, if the 0 of the main scale don’t coincide with that of Vernier scale then it is an instrumental error as the design of Vernier calliper is not proper
Random Errors: Random Errors are not fixed on general perimeters and depend on measurements to measurements. That’s why they are named Random errors as they are random in nature. Random errors are also defined as fluctuations in statistical readings due to limitations of precisions in the instrument. Random errors occur due to:
- Sudden and unexpected shifts in experimental conditions of the environment
- Personal bias errors which even the student is unaware of
Example:
- A spring balance will give different readings if the temperature of the environment is not constant
- If a person repeats an experiment he is more likely to get different observations.
