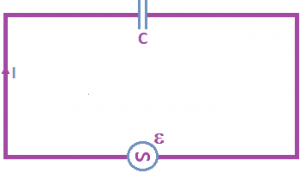
AC Voltage Source Applied Across a Capacitor
The purpose of a capacitor is to store energy in the form of an electrical charge, on its plates. When a capacitor is connected across a DC supply voltage it charges up to the value of the applied voltage at a rate determined by its time constant. We have a capacitor and an AC voltage V, represented by the symbol “~”, that produces a potential difference across its terminals that varies sinusoidally. Here, the potential difference or the AC voltage can be given as, v = vm sinωt.
Where,
vm = Amplitude of the oscillating potential difference.
ω = Angular Frequency.
The current through the resistor due to the present voltage source can be calculated using the Kirchhoff’s loop rule, as under ΣV (t) = 0.
From the above Circuit, We can write v = q/ c.
According to the Kirchhoff’s rule, we can write from the above circuit, vm sinωt = q/ c.
The current through the circuit can be calculated using the relation,
\(i\,=\,\frac{dq}{dt}\),
\(i\,=\,\frac{d({{v}_{m}}\,C\,\sin \,\omega t)}{dt}\,=\,\omega \,C\,{{v}_{m}}\,\cos \,\omega t\),
\(i\,=\,{{i}_{m}}\,\sin \,\left( \omega t+\frac{\pi }{2} \right)\,\) \(\left( \because \,\cos \,\omega t\,=\,\sin \,\left( \omega t+\frac{\pi }{2} \right) \right)\).
Here the amplitude of the current can be written as, im = ωCvm.
Or else we can write it as \({{i}_{m}}\,=\,\frac{{{v}_{m}}}{\frac{1}{\omega \,C}}\).
Here, we can see that the term 1/ωC can be said to be equivalent to the resistance of this device and is termed as the capacitive resistance. We denote the capacitive resistance of the device as XC.
\({{X}_{C}}\,=\,\frac{1}{\omega C}\).
And thus, we can say that the amplitude of current in this circuit is given as \({{i}_{m}}\,=\,\frac{{{v}_{m}}}{{{X}_{C}}}\).
In the above equations, the dimension of the capacitive resistance can be seen to be the same as that of resistance and also, the SI unit of capacitance is given as ohm. The capacitive resistance restricts the passage of current in a purely capacitive circuit the same way as resistance hinders the passage of current in a purely resistive circuit. Here we say, that the capacitive resistance is inversely proportional to the frequency and the capacitance. We also see from the above equations that the current in a capacitive circuit is π/2 ahead of the voltage across the capacitor. The instantaneous power supplied to the capacitor can be given in terms of the current passing through the capacitor as PC = i v im cosωt vm sinωt.
\({{P}_{C}}\,=\,\frac{{{i}_{m}}\,{{v}_{m}}}{2}\,\sin \,2\omega t\).
Here, the average power supplied over a complete cycle can be given as \({{P}_{C}}\,=\,\frac{{{i}_{m}}\,{{v}_{m}}}{2}\,\sin \,2\,\omega t\,=\,0\).
Concluding the article, we can say that in the case of a capacitor the current leads the voltage by π/2.
