Horizontal Range of the Escaping Liquid

Horizontal Range of the Escaping Liquid

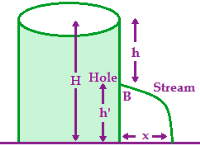
Water stands at a depth H in a tank whose sides are vertical. A hole is made in one of the walls at a depth h below the water surface. Let container remains at rest. When the liquid remains emerges out of the hole, it goes along a parabolic path. So, time taken by water to fall through a height of H – h is given as:

H – h = 0 x t + ½ gt²

\(t=\sqrt{\frac{2(H-h)}{g}}\).

\(V\times t=\sqrt{2gh}\sqrt{\frac{2(H-h)}{g}}=\sqrt{4h(H-h)}=2\sqrt{h{{h}^{‘}}}\).

Horizontal range is given by:

\(x=\sqrt{4h(H-h)}\).

\(x=\sqrt{4hH-4{{h}^{2}}+{{H}^{2}}-{{H}^{2}}}\).

\(x=\sqrt{{{H}^{2}}-({{H}^{2}}-4hH+4{{h}^{2}})}\).

\(x=\sqrt{{{H}^{2}}-{{(2h-H)}^{2}}}\).

For the range to be maximum, (2h – H)² = 0

(2h – H) = 0

h = H/2

So, the maximum range, \(x=2\sqrt{h{{h}^{‘}}}\).

The formula \(x=2\sqrt{h{{h}^{‘}}}\) tells us if we make two holes at equal vertical distances from top and bottom, both liquids jets will strike the same spot but not simultaneously.