Pole and Polar
Polar of a Point with Respect to a Circle: If through a point P(x₁, y₁) (within or without a circle) there be drawn any straight line to meet the given circle at Q and R the locus of the point of intersection of the tangents at Q and R is called the polar of P and P is called the pole of the polar.
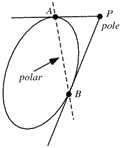
The polar of a point P(x₁, y₁) with respect to the circle x² + y² = a² is xx₁ + yy₁ = a².
The polar of P(x₁,y₁) with respect to the circle x² + y² +2gx + 2fy + c = 0 is xx₁ + yy₁ + g(x+x₁) + f(y+y₁) + c = 0 which is same as the equation of the tangent at P(x₁,y₁) if P(x₁,y₁) lies on the circle.
Pole of a given line Ax+By+C=0 with respect to circle x² + y² = a² is \(\left[ \frac{-A{{a}^{2}}}{C},\frac{-B{{a}^{2}}}{C} \right]\).
Properties of Pole and Polar:
- The distance of any two points P(x₁, y₁) and Q(x₂, y₂) from the centre of a circle are proportional to the distance of each from the polar of the other.
- If the polar of a point P(x₁, y₁) with respect to a circle whose centre is O meets the straight line joining P to the centre of the circle in the point Q, then
a) OP is perpendicular to the polar of P
b) P and Q are inverse points with respect to the circle i.e., OP.OQ = (radius)²
Example: The pole of a straight line with respect to the circle x² + y² = a² lies on the circle x² + y² = 9a² prove that the straight line touches the circle x² + y² = a²/9
Solution: Let P(x₁, y₁) be the pole of the given straight line with respect to x² + y² = a² Then the equation of the polar i.e., the straight line is xx₁ + yy₁ = a² …1
It is given that P(x₁, y₁) lies on x² + y² = 9a²
x₁² + y₁² = 9a²
Now, length of the perpendicular from the centre (0, 0) of the circle \({{x}^{2}}+{{y}^{2}}=\frac{{{a}^{2}}}{9}\) on (1), is \(\left| \frac{0{{x}_{1}}+0{{y}_{1}}-{{a}^{2}}}{\sqrt{x_{1}^{2}+y_{1}^{2}}} \right|=\frac{{{a}^{2}}}{\sqrt{x_{1}^{2}+y_{1}^{2}}}=\frac{{{a}^{2}}}{\sqrt{9{{a}^{2}}}}=\frac{a}{3}\)
Clearly, length of the perpendicular from the centre O(0, 0) of the circle \({{x}^{2}}+{{y}^{2}}=\frac{{{a}^{2}}}{9}\) to the line (1) is equal to the radius of the circle.
Hence, the straight line touches the circle .
Important points:
i) If the point P is an exterior point of the circle then the chord of contact of P will be the polar of P.
ii) If P lies on the circle then the polar of P coincides with the tangent at P.
iii) If P is inside the circle then the polar of P does not intersect the circle.
iv) The pole of with respect to S = x² + y² + 2gx + 2fy + c = 0 is \(\left[ -g+\frac{l{{r}^{2}}}{\lg +mf-n},\,\,-f+\frac{m{{r}^{2}}}{\lg +mf-n} \right]\) where r is the radius of the circle.
